Complexidade Logarítmica O(log n)
- #GoLang
Back to school, vamos falar de matemática mas é algo tão simples que nem vai da tempo de você fica chateado.
É necessário entender um pouco sobre Logaritmos para entender a próxima notação, basicamente o que você precisa ter em mente é que logaritmos são o inverso de exponenciais.
E talvez você esteja lendo isso e “eu já vi isso na faculdade e etc”, eu não vi isso na faculdade porque eu não fiz faculdade eu tenho estudado isso por conta própria.
Se você também tá estudando por conta própria e acha que saber sobre complexidade, estrutura de dados não vai fazer diferença eu tomaria mais cuidado ou pelo menos investiria em soft skills para compensar o débito acadêmico. Quando você fizer um teste possivelmente alguém que faz ciências da computação vai disputar a vaga com você e ela já conhece isso por padrão.
Isso é um logaritmo:
log2(8) = 3
Leia-se, log na base 2 de 8 é igual a 3 e porque é igual a 3?
Porque a pergunta desse logaritmo é “qual numero eu uso na exponenciação para 2 que resulta em 8?”.
Então será 3 porque 2³ (dois ao cubo) é 2 * 2 * 2 = 8 fim do mistério.
E porque logaritmos são o inverso da exponenciação? Pois através do logaritmo de N temos o numero de operações.
O numero de operações é:
log 2(n) = x
Onde x é o numero de operações realizadas durante a execução do algoritmo.
Infelizmente nem tudo são flores e nem todo logaritmo é na base de 2 mas esse calculo não é a parte mais importante, repare que até aqui falamos sobre as complexidades e elas tem exemplos matemáticos como a exponenciação mas não fazemos contas realmente pra chegar na notação do algoritmo.
Então, para uma lista de 8 números, você teria que verificar 3 números no máximo. Para uma lista de 1.024 elementos, log 1.024 = 10, porque 2 elevado a 10 == 1.024. Então, para uma lista de 1.024 números, você tem que verificar 10 números no máximo.
Um exemplo de algoritmo com complexidade O(log n) é uma busca binária em uma lista já ordenada.
package main
import "fmt"
func main() {
arr := []int{2, 3, 4, 10, 40}
item := 9
busca := buscaBinaria(arr, 0, len(arr), item)
fmt.Println(busca)
}
func buscaBinaria(arr []int, esquerda, direita, item int) bool {
for esquerda <= direita {
meio := esquerda + (direita-esquerda)/2
if arr[meio] == item {
return true
}
if arr[meio] < item {
esquerda = meio + 1
} else {
direita = meio - 1
}
}
return false
}
Esse tipo de algoritmo é bem simples você parte o input ao meio e ai compara pra verificar se o item a ser buscado é menor ou maior que o item no meio do array. Quando isso acontece você joga fora metade da lista ficando com uma parte menor e esse processo é repetido até que se encontre o item da busca diminuindo cada vez mais o processamento, por isso ele é o inverso do exponencial você diminui o N toda vez que um processamento é feito.
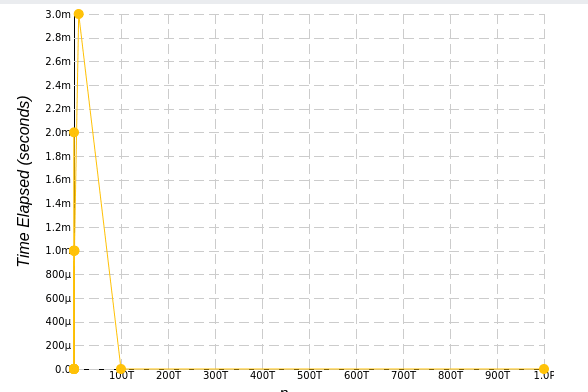
Nesse exemplo do gráfico da pra verificar que o numero varia muito porém o tempo é irrelevante em relação a outras complexidades ali em baixo o input é de 1pb e o tempo de 3 milésimos. O gŕafico mostra como N aumenta e logo em seguida se torna quase uma constante, isso acontece porque mesmo que N duplique o algoritmo sempre vai estar fatiando N pela metade várias vezes até encontrar o resultado.
Como um rapaz disse no tweet que em que perguntei sobre log n esses dias “como você explicaria log n para um Júnior/Sandy”, ele disse:
Vou deixar aqui o link do Tweet pra quem quiser ver mais sobre Log N pois tiveram diversos pontos de vista sobre e podem ajudar mais pessoas.
Esse exemplo da busca binária só funciona quando se tem uma lista ordenada caso contrário o algoritmo não poderia garantir que o elemento procurado está de fato em uma metade ou outra da lista, sendo necessária outra abordagem.
Complexidade Quadrática: