Você se preocupa com como escreve suas queries?
- #NoSQL
- #SQL
- #SQLite
Estou estudando Análise de Cálculo para Sistemas e venho trazer meus 2 palitos de conhecimento com exemplos práticos e aplicabilidade da teoria com exemplos praticos do nosso dia a dia de desenvolvedores...
Um exemplo simples:
>>> SELECT * FROM my_table WHERE ID = 44;
Vamos supor que sua tabela tenha 8 elementos:
1 | 12 | 15 | 27 | 30 | 44 | 50 | 51
Queremos achar o número 44. Caso você não tenha um índice para esta "tabela", teremos que percorrer elemento por elemento até chegar em 44. Chamamos isso de força bruta.
Ok, mas como um índice faz para otimizar esse tipo de busca? Vamos mais a fundo nos fundamentos da programação, minha parte favorita!
Os bancos de dados utilizam normalmente uma árvore B, ou B-tree em inglês. Para simplificar a explicação, uma árvore B é uma generalização de uma árvore binária de busca, que nos permite utilizar a busca binária, ou Binary Search em inglês. Um algoritmo clássico que você precisa conhecer!
Você sabe como a busca binária funciona?
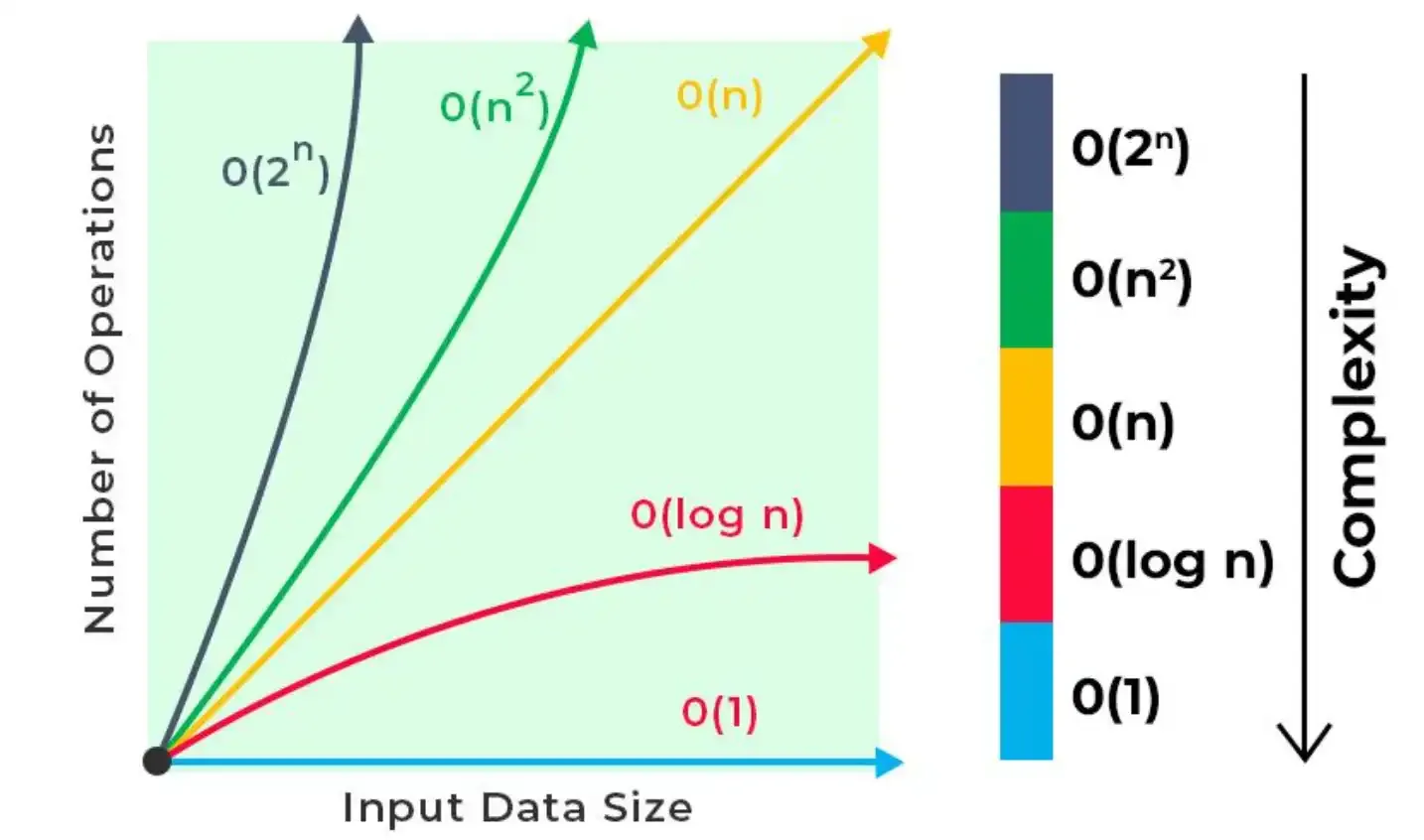
Filtrando por um campo não indexado, no pior caso, temos que percorrer toda a nossa tabela, nesse caso a complexidade dessa operação é O(n), onde n é o número de registros dessa tabela. Na busca binária, os elementos devem estar ordenados e a cada iteração, nosso problema é dividido ao meio.
1️⃣ O algoritmo sempre inicia pegando o elemento do meio, nesse caso 8 / 2 = 4. Lembre-se que iniciamos do índice 0, nesse caso o número 30:
1 | 12 | 15 | 27 | 30 | 44 | 50 | 51
2️⃣ Sabemos que o número 44 é maior do que o número 30, então vamos apenas olhar para os registros da direita utilizando o mesmo conceito, sempre iniciar pelo elemento do meio, nesse caso o número 50:
44 | 50 | 51
3️⃣ 50 eh maior do que 44, então fazemos o mesmo com os elementos da esquerda. Só temos um elemento e é exatamente o número que estamos buscando!
A "tabela" que listei acima tem 8 elementos. No pior caso, quantas iterações precisamos utilizando a busca binaria?
Ao invés de 8 iterações utilizando força bruta, você só precisou de 3.
Ok, e qual o custo computacional dessa operação? O(lg n)
Quando falamos de Big O, falamos de base 2. log de 8 na base 2 é igual a 3 (2^3 = 8).
Passamos de O(n) para O(lg n). O tempo de busca foi DRASTICAMENTE reduzido.
Tá vendo a importância de entender os fundamentos? :)
Uma boa hora para rever suas queries e reavaliar os índices que você precisa criar!
https://miro.medium.com/v2/resize:fit:678/0*ouBkTMgA_yg_Etfz.png