Tudo o que você precisa saber sobre Algoritmos e Estrutura de Dados
- #Estrutura de dados
Algoritmo é que um conjunto de instruções que realizam uma determinada tarefa. Eles são uma das bases da programação. Pensando em um exemplo, para fazermos uma receita culinária, nós precisamos dos ingredientes e de um conjunto de instruções, descrevendo o passo a passo para a sua confecção, que podemos chamar de algoritmo. Através dos algoritmos, escrevemos instruções para que os computadores possam resolver um problema específico.
Estrutura de dados é o ramo da computação que estuda os diversos mecanismos de organização de dados para atender aos diferentes requisitos de processamento, ou seja, é a forma como organizamos os dados.

Fonte: https://hermes.dio.me/articles/cover/f670c93c-86d8-4207-ac79-93ecce3a3ba8.jpg
Imagine que temos uma tabela com um milhão de registros e precisamos encontrar um determinado valor nela. Se buscarmos esse valor de forma sequencial, podemos demorar até um milhão de passos para encontrar o dado que queremos (considerando o pior caso, caso esteja na última posição). Por isso, é importante estruturarmos os dados de forma eficiente, além de utilizar algoritmos eficientes, para otimizar nossos serviços. Esse é um tópico extremamente importante, que todo programador precisa conhecer para evoluir na carreira.
Neste artigo, preparei um resumo com as principais estruturas de dados utilizadas. Se vocês gostarem desse conteúdo, posso escrever outros artigos com a implementação dos algoritmos descritos, em Java ou Kotlin. Não deixem de me seguir e interagir com esse conteúdo, para que eu possa trazer mais conteúdos de programação e tecnologia.
Notação Big O (Big-O Notation)
A notação Big O é uma notação especial que diz o quão rápido é um algoritmo, sendo utilizada para comparar o número de operações necessárias para um algoritmo encontrar um determinado elemento em uma busca. Esta notação leva em conta a pior cenário de busca (caso não encontre o elemento ou ele esteja na última posição do array), apesar de também ser necessário estudar o tempo de execução para o “caso médio”, na comparação dos algoritmos de busca.
O O(1) representa o algoritmo perfeito, onde precisaríamos de apenas um passo para encontrar um elemento qualquer, independentemente do tamanho do array (representado pela cor verde, na imagem abaixo). Já o O(n!) representa os piores algoritmos, onde a quantidade de passos necessários para se encontrar determinado elemento aumenta de forma fatorial, de acordo com a quantidade de elementos presentes no array (n é o tamanho do array.) Na imagem a seguir, é representado pela linha vertical esquerda, dentro da cor rosa.
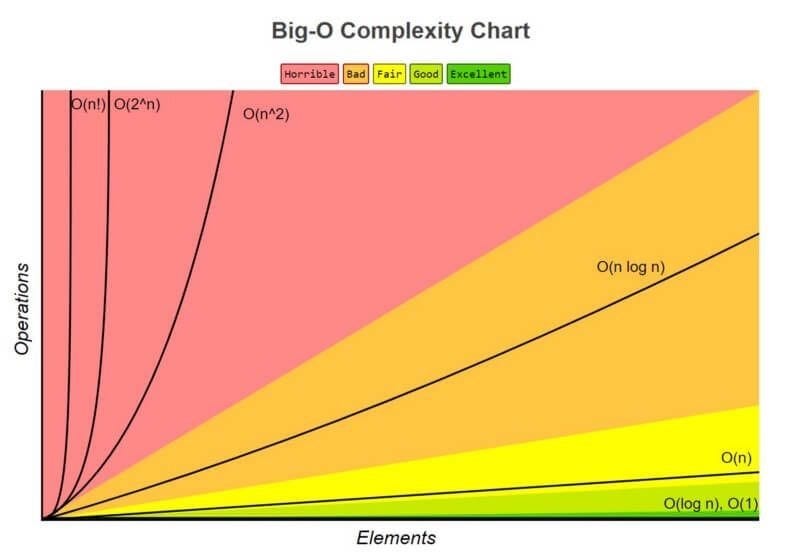
Fonte: https://www.freecodecamp.org/portuguese/news/content/images/2021/12/1_KfZYFUT2OKfjekJlCeYvuQ.jpeg
Algoritmos de Busca
Busca Linear (Linear Search)
É um algoritmo que busca elementos de um array de forma sequencial (do início para o fim ou do fim para o início). Como ele busca os elementos um a um, é um algoritmo bem lento, sua complexidade é O(n). Vamos ver um exemplo onde queremos buscar o elemento 3 em um array que contém 5 elementos, a busca linear ficaria assim:
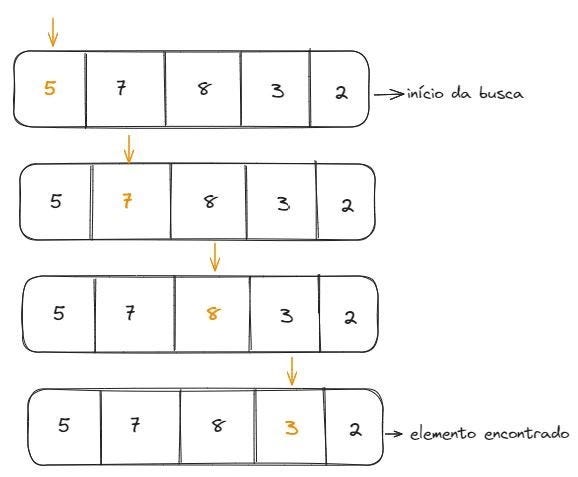
Como o elemento estava na penúltima posição do array, foi preciso realizar quatro passos até encontrá-lo.
Busca Binária (Binary Search)
A busca binária só funciona quando a lista está ordenada (em sequência crescente) e é um dos algoritmos mais performáticos para buscas. Quando queremos verificar se um determinado elemento está em um vetor e em qual posição, podemos utilizar este algoritmo. Para realizar a busca, o primeiro passo é buscar um elemento qualquer no vetor (normalmente, buscamos o elemento que está no meio) e verificar se este elemento é maior ou menor que o elemento que estamos buscando. Se o valor procurado for maior que o elemento que estamos comparando, o algoritmo vai eliminar a metade da lista que está a sua esquerda. Caso o elemento procurado for menor que o elemento que estamos comparando, então vai eliminar a metade da lista que está a sua direita. Em seguida, vamos repetir essa sequência até encontrar o elemento desejado, sempre eliminando metade das possibilidades a cada passo.
Caso o elemento que estamos buscando estiver na lista, a busca binária retornará sua localização. Mas, caso o elemento não seja encontrado, a busca vai retornar None. A desvantagem algoritmo é que a lista precisa estar ordenada para poder fazermos a busca. Por isso que, normalmente, escolhemos o elemento que está no meio do vetor para realizar a comparação, já que isso elimina metade das possibilidades a cada passo.
Vamos pensar em um exemplo, se temos 100 elementos em uma lista e estamos buscando o 63, primeiro o algoritmo vai buscar no elemento 50. Como 63 está acima de 50, vamos eliminar todos os elementos que estão a sua esquerda (menores que 50). Em seguida, vamos buscar novamente o número 63 comparando-o com o elemento que está no meio do array, que é o número 75. Como 63 é menor que 75, dessa vez vamos eliminar todos os elementos que estão à sua direita (maiores que 75). Depois, continuamos a pesquisar o elemento no array que restou até o encontrarmos ou sobrar apenas um elemento no array.
De maneira geral, para uma lista de n números, a pesquisa binária precisa de log(2n) para retornar o valor correto, enquanto a pesquisa simples precisa de n etapas. A complexidade desse algoritmo é de O(log n). Utilizando o mesmo exemplo da busca linear, vamos buscar o elemento 3 no mesmo array que usamos na pesquisa linear (após ordenar o array):
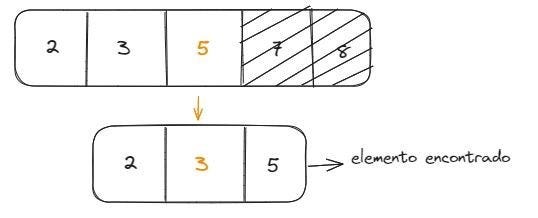
Como podemos ver, foi necessários apenas dois passos para encontrar o elemento utilizando busca binária, enquanto na busca linear foram necessários 4 passos.
Pilha (LIFO — Last in, first out)
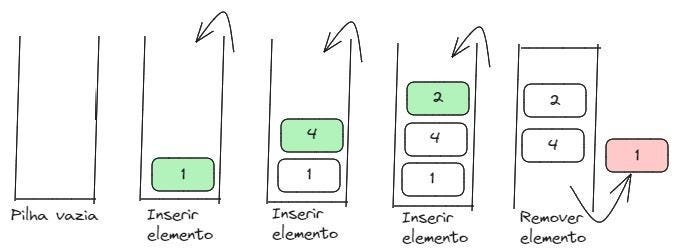
A pilha é considerada um tipo abstrato de dados, pois não precisa de nada novo para armazenar os dados. É baseada na lista encadeada, onde o último elemento inserido será o primeiro que será lido (não é possível pesquisar algum elemento no meio de uma pilha, por exemplo). Os métodos possíveis para manipulação de uma pilha são:
- Método Top: utilizado para verificar qual é o primeiro elemento da pilha (que está no topo). Por exemplo, pilha.top() recebe a referência do topo da pilha;
- Método Pop: tira, de fato, o primeiro elemento da pilha. Por exemplo, pilha.pop(), após remover o elemento, a referência de topo passa para o próximo elemento da pilha;
- Método Push: adiciona um novo elemento na pilha;
- Método isEmpty: verifica se a referência para a entrada da pilha está nula (ou seja, se há ou não uma pilha);
Vejamos um exemplo de Pilha:
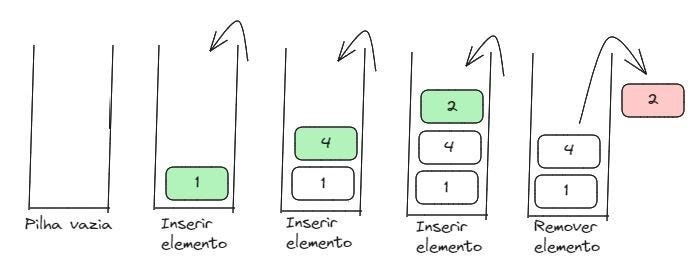
Fila (FIFO — First in, first out)
Também é considerado um tipo abstrato de dado (por exemplo, é possível criar uma fila utilizando uma lista ligada, um vetor, etc.). Na fila, o primeiro elemento inserido será o primeiro a ser lido (como ocorre em uma fila qualquer como, por exemplo, em uma fila de banco, onde o último que entrar será o último a ser atendido). Vejamos um exemplo:
Algoritmos de Ordenação
Vetor (Array)
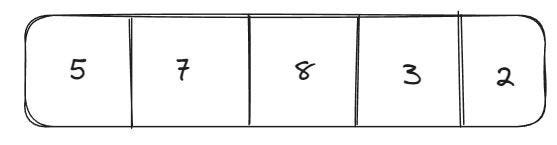
O vetor é considerado um tipo de lista (representado por um objeto) que permite armazenar diversos elementos. Os elementos são inseridos de acordo com o índice e possui um tamanho fixo. Caso precise adicionar novos elementos, mas não tiver mais espaços livres, será preciso criar um novo array com tamanho maior que o anterior, depois precisamos copiar todos os elementos do array antigo para o novo e, por fim, adicionar os novos elementos ao novo array. Por conta disso, o array é considerado rápido para realizar buscas, mas lento para inserção e deleção de elementos. Vejamos uma representação de um array:
Lista Encadeada (ou Ligada)
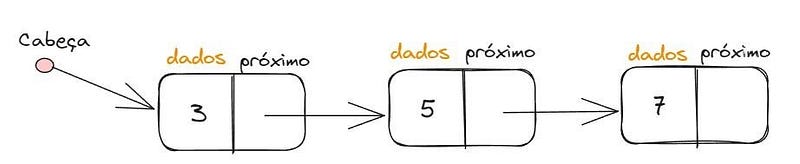
É uma lista de tamanho dinâmico, onde cada elemento conhece o endereço do elemento predecessor. Seu funcionamento é similar ao do array, porém, é recomendada sua utilização quando for preciso realizar muitas inserções e não sabemos qual o total de elementos a ser inserido. Porém, quando é necessário buscar um elemento, é preciso começar buscando o primeiro elemento, que vai buscar o segundo, que vai buscar o terceiro, e assim por diante, até encontrar o elemento desejado. Ou seja, ele é muito rápido para inserções, mas lento para buscas.
É possível utilizamos o iterator, que é um padrão utilizado para buscar elementos dentro de uma lista. O iterator guarda apenas o elemento atual e possui métodos para verificar se há mais elementos naquela lista. Vamos ver um exemplo:
Lista Duplamente Encadeada
É utilizada quando precisamos seguir a sequência de elementos em ambos os sentidos. Ou seja, cada elemento vai conhecer o elemento anterior e o predecessor. Exemplo:

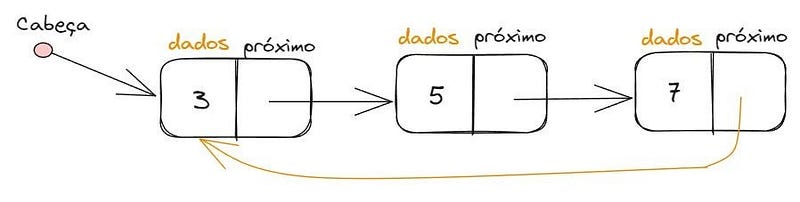
Listas Circulares
É quando o último elemento da lista aponta para a referência do primeiro elemento. Sendo que, o último elemento é chamado de “Cabeça” e o primeiro de “Cauda”. Temos também uma referência de entrada para o primeiro nó, onde entramos na lista pela Cauda. Os métodos utilizados são remove(element), get(index), add(element) e isEmpty(). Exemplo:
Ordenação Bolha (Bubble Sort)
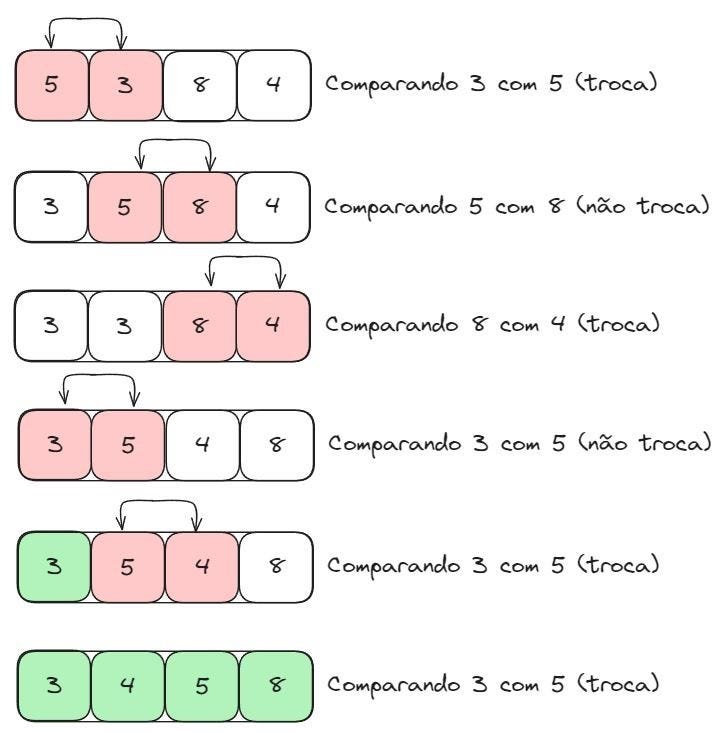
É um algoritmo de ordenação que funciona comparando dois elementos de cada vez: um elemento fica “parado”, enquanto um ponteiro percorre o vetor comparando o elemento que está parado com esse elemento da vez. Caso o elemento apontado for menor que o elemento índice (que está parado), movemos ele para antes desse elemento.
Quando o ponteiro percorrer todos os elementos daquele vetor, o próximo elemento será o índice e o ciclo irá recomeçar, até que todos os elementos estejam ordenados corretamente. Por conta do seu funcionamento, este algoritmo é considerado bem lento, sendo a complexidade do pior caso O(n^2) .
Pensando em sua implementação em uma linguagem como Java ou Kotlin, podemos utilizar um laço de repetição for com um elemento i, que será o nosso elemento índice, e dentro deste loop criamos um outro laço for com um elemento j, para ser o ponteiro com o elemento que vamos comparar, em cada passo. Vamos ver um exemplo:
Ordenação Rápida (Quick sort)
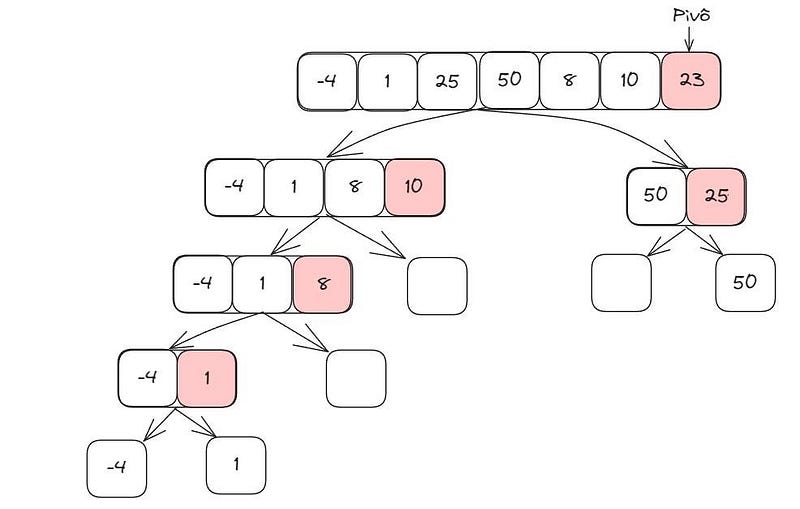
É considerado um dos algoritmos de ordenação mais rápido. O Quick Sort funciona através da estratégia de dividir o problema em problemas menores, diminuindo a quantidade de comparações. Ao invés de ordenar o vetor inteiro, declaramos um elemento como pivô (normalmente, é escolhido o elemento do meio) e, os elementos menores que ele vai ficar do seu lado esquerdo, e os vão maiores que eles vão ficar do seu lado direito. Após isso, cada lado será considerado um subarray e um novo elemento será definido como pivô, em cada um dos subarrays, e o processo será reiniciado (elementos menores que o pivô para o lado esquerdo e os maiores para o lado direito). Isso é feito recursivamente, até todos os elementos serem ordenados. Considerando seu pior caso, possui uma complexidade de O(n^2) e, considerando a média, tem uma complexidade de O(log n) . Vejamos um exemplo:
Ordenação por seleção (Selection Sort)
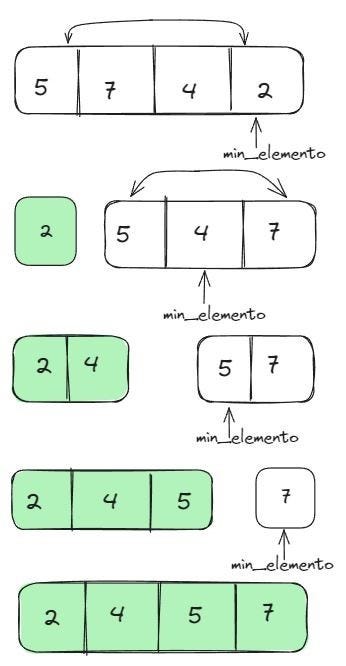
É um algoritmo de ordenação que compara o elemento a ser ordenado com cada um dos elementos da lista, um a um. Ou seja, se ele encontrar um elemento menor que ele, vai movê-lo para o início do vetor, colocando-o na sequência correta. Vamos ver um exemplo:
Ordenação em Heap (Heap Sort)
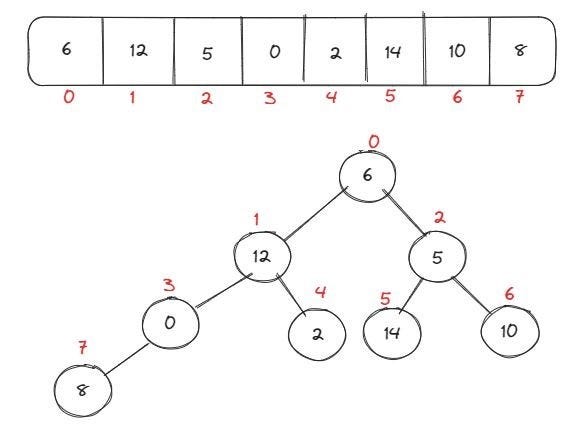
É um algoritmo de ordenação do tipo árvore, em que o elemento pai sempre será maior que o filho que está a sua direita e menor que o filho que está a sua esquerda. Em um heap máximo, sempre o elemento pai será maior do que seus filhos. Para montar a árvore de acordo com os elementos do array, utilizamos a fórmula: 2i + 1 . Após ordenar os filhos da árvore, o algoritmo é chamado novamente, de forma recursiva, até ordenarmos todo o vetor corretamente. Exemplo:
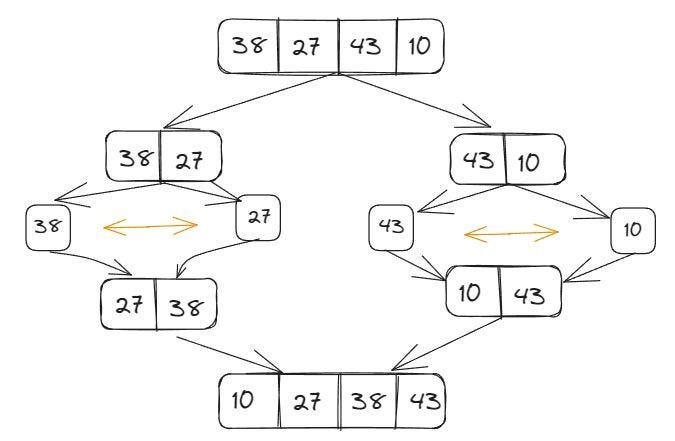
Ordenação por Intercalação (Merge Sort)
A ideia básica deste algoritmo é intercalar duas metades de uma lista que já estão ordenadas. Funciona com base na recursão, utilizando a estratégia de dividir para conquistar. O problema é quebrado em subproblemas, que são similares ao problema original. Recursivamente, o algoritmo resolve os subproblemas e, depois, combina as soluções para resolver o problema original. Exemplo:
Ordenação por Inserção (Insertion Sort)
Seu funcionamento é bem simples, tendo uma complexidade similar à do Bubble Sort. Este algoritmo é utilizado quando precisamos inserir um novo elemento em um vetor que já está ordenado. Primeiro, precisamos aumentar o tamanho do vetor em um (lenght+1), em seguida, precisamos verificar se o elemento a ser inserido é menor que o primeiro elemento do array. Caso seja, esse elemento inserido passa a ocupar essa posição e passa os demais elementos para frente. Caso contrário, ele passa a comparação para o elemento seguinte, até encontrar o elemento menor que ele, ou então assume a última posição no array. Sua complexidade para o melhor caso é de O(n) e, para o pior caso, é de O(n^2) . Exemplo:
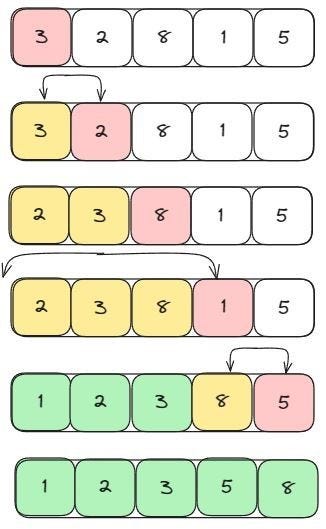
Tabela de Dispersão (Hash Table)
A tabela de dispersão (hash table) é uma estrutura de dados especial, que associa chaves de pesquisa a valores de busca de um vetor não-ordenado. Quando precisamos inserir um novo elemento dentro de uma tabela hash, precisamos utilizar uma função matemática que vai gerar um índice válido no array, com base no valor do elemento a ser inserido. A essa função damos o nome de função hash / função de espalhamento / função mapeamento. Usando essa função, conseguimos mapear as chaves para os índices do array e armazenar os objetos (que são chamados de valores) em pares de <chave, valor>. Para criarmos uma função hash, precisamos levar em consideração as seguintes regras:
- Deve ser determinística. Ou seja, para uma determinada chave, a função sempre retorna o mesmo valor de hash;
- Deve ser sempre executada em tempo constante O(1) ;
- Deve sempre retornar um valor de hash dentro dos limites da tabela [0,N−1] , onde N é o tamanho da tabela.
Esta estrutura de dados é considerada muito rápida, tanto para buscas, quanto para inserções. Vamos pensar em um exemplo onde queremos armazenar os nomes de algumas pessoas em uma tabela hash. Primeiramente, precisamos criar uma função hash, que será responsável por calcular o índice (posição), de onde o elemento será armazenado. Para a função, podemos pegar o tamanho de cada nome (string) e transforma-lo em um número inteiro, subtraindo um, que pode ser representada pela seguinte fórmula: índice = quantidade_de_letras − 1.
Vamos inserir os nomes Bia, Caio, Paula, Carlos e João nessa tabela. Aplicando a função para nome, receberemos os seguintes índices:
- Bia = 3 letras — 1 = índice 2;
- Caio = 4 letras — 1 = índice 3;
- Paula = 5 letras — 1 = índice 4;
- Carlos = 6 letras — 1 = índice 5;
- João = 4 letras -1 = índice 3;
Como podemos notar, quando calculamos o índice para o João, recebemos o mesmo valor que o do Caio. Isso significa que, quando tentarmos inserir o João na tabela, teremos uma colisão. Após as inserções, nossa tabela vai ficar assim:
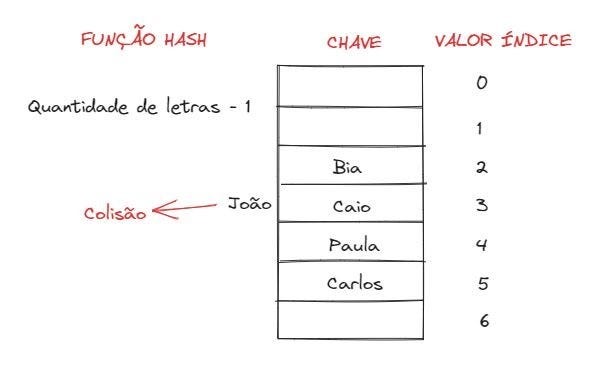
Para buscar um elemento, basta aplicar a função novamente, passando o nome e recebendo a posição. Por exemplo, para buscar a Bia, sabemos que o tamanho do nome é 3 e que, aplicando a fórmula, teremos o índice 2 como resposta. De acordo com a tabela, podemos ver que na posição 2 se encontra exatamente a Bia. Caso ele não encontrasse a Bia nesta posição, significa que ela não está na tabela. E, caso encontrasse outro nome, significa que houve uma colisão e existem mais nomes naquele índice. Uma função hash é considerado boa se ela for capaz de:
- Produzir um baixo número de colisões;
- Ser facilmente computável (não levar um tempo muito elevado para calcular o índice de um novo elemento);
- Ser uniforme (levar um tempo constante para transformar qualquer chave em um valor).
Para sabermos se uma função hash é boa, podemos calcular o seu fator de carga, que é a quantidade de elementos de uma tabela hash, dividido pelo tamanho do vetor (levando em conta que o tamanho do vetor precisa ser maior que o número de elementos). Por exemplo, se temos 4 elementos e um vetor de 6 posições, teremos o seguinte fator de carga: Fc = 4/6 = 0,67.
Quanto mais perto do 1 o fator de cargo estiver, menos espaços vazios vamos ter na tabela, o que pode gerar mais colisões. E, quanto mais perto estiver do 0, teremos uma grande quantidade de espaços vazios, o que diminui a possibilidade de colisões. Porém, isso significa que teremos um maior desperdício de memória, com muitos espaços não utilizados do vetor.
Quando ocorrer uma colisão, existem basicamente duas estratégias para resolução:
- Encadeamento Exterior ou Separado
— Listas encadeadas.
- Encadeamento Interior ou Aberto
— Heterogêneo;
— Homogêneo (Teste Linear).
No encadeamento exterior com listas encadeadas vamos armazenar os elementos fora do array, utilizando ponteiros. Quando um elemento for adicionado ao vetor, vamos calcular o seu índice de acordo com a função hash e, ao invés de colocar este elemento diretamente na posição, criamos uma lista encadeada externa, colocando o novo elemento como a primeira posição da lista. E, na posição do array referente aquele índice, teremos um ponteiro que indicará qual o endereço daquela lista encadeada. Cada elemento da lista encadeada (nó) possui duas informações, o valor armazenado e o endereço para o próximo elemento da lista. Quando um índice do array não tiver um ponteiro ou um elemento da lista não tiver o endereço para o próximo, retornaremos um nulo, indicando que não há mais valores naquela lista. Quando um elemento for removido de uma lista encadeada, o elemento anterior a ele terá o endereço para o próximo atualizado, apontando para o elemento posterior ao que foi removido.
Pensando em um exemplo, vamos criar uma tabela hash com seis posições. Para isso, precisamos primeiro criar uma função que vai utilizar o módulo seis (pois é o tamanho do vetor) do elemento a ser inserido, retornando um número inteiro (índice). Agora, vamos inserir os números 12, 21, 10, 9 e 33 nessa tabela:
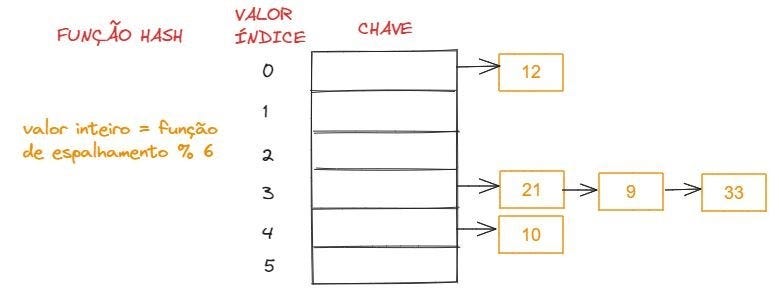
No encadeamento interior heterogêneo temos um vetor com algumas posições a mais, que é onde iremos inserir os elementos que colidirem. Ou seja, quando ocorrer uma colisão, o elemento será inserido no próximo espaço reservado vazio. Para fazer a busca, primeiro utilizamos a função hash para calcular o índice. Caso o número retornado não esteja no índice, significa que precisamos procurá-lo por ele dentro do espaço reservado a colisões, onde iremos procurá-lo de forma sequencial. Por conta disso, se tivermos muitas colisões na tabela hash, a busca ou remoção de um elemento ficará muito mais lenta, pois terá o mesmo tempo de execução que a busca sequencia).
Quando removermos um elemento, diferenciamos aquele espaço de uma outra forma (como, por exemplo, colocando um número negativo) pois, se durante a busca o algoritmo entrar no espaço de colisão e se deparar com um espaço vazio, vai interromper a busca e retornar que o elemento não foi encontrado. Vamos ver um exemplo:
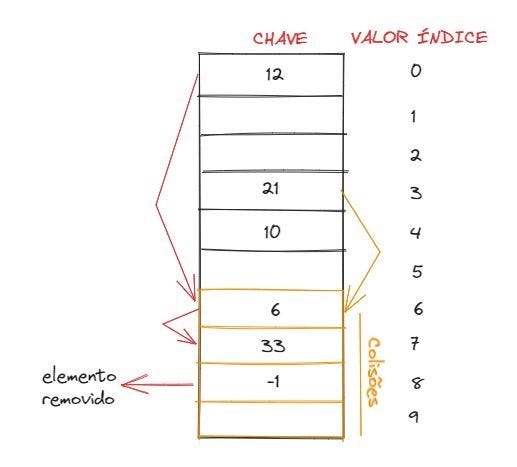
No encadeamento interior homogêneo, quando ocorre uma colisão, vamos utilizar o teste linear, inserido o elemento no próximo que espaço vazio ou disponível. Como no tipo anterior, se houver muitas colisões, o algoritmo de busca/remoção ficará com a mesma velocidade que a busca sequencial.
Como as tabelas hash são arrays (possuem um tamanho fixo), não conseguimos adicionar mais elementos que a quantidade de espaços disponíveis. Para resolver isso, precisamos criar uma tabela maior que a original e realocar os elementos para essa nova tabela. A isso damos o nome de resize. É importante mencionar que, os elementos não serão alocados nas posições originais, pois ao criar uma nova tabela, precisamos criar uma nova função hash (já que o tamanho do array mudou e a função usa esse número como base). A criação dessa nova função é chamada de rehash.
Árvores
Uma árvore é uma estrutura de dados bidimensional, não linear e constituída de nós que representam um modelo hierárquico (armazenam os dados com base em relações de dependências). Elas são formadas por nó, raiz e folhas. Seu elemento inicial é chamado de raiz e seus filhos são chamados de folhas.
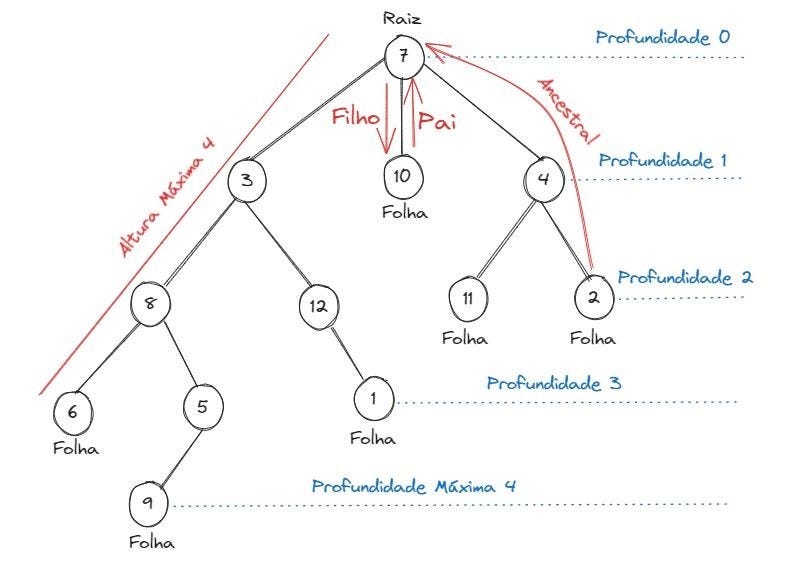
A altura de um nó é a distância desse nó até a raiz. Um conjunto de nós com a mesma profundidade é denominado nível da árvore e a maior profundidade de um nó é a altura ou profundidade máxima da árvore. E o ponteiro de um nó é a distância do nó até a raiz. A árvore é sempre estruturada através de uma ordem (por exemplo, se os elementos da esquerda forem menores que o elemento raiz, os elementos da direita serão maiores que ele). Em uma árvore, cada elemento possui três informações: o seu próprio valor, um ponteiro para o nó da esquerda e outro ponteiro para o nó da direita. Quanto mais relações um elemento tem, mais ponteiros para os nós ele terá. Quando um elemento não tem um próximo elemento associado a ele, ele é chamado de nó folha. Seja x um vértice (nó) de uma árvore com raiz (r), temos a ancestralidade da árvore como:
· Ancestral: é qualquer nó y no caminho de r a x;
· Descendente: x é uma descendente de y se y é ancestral de x;
· Filho: x é filho de y se ele tem é um descendente direto;
· Pai: é o ancestral mais próximo. A raiz é o único nó sem pai;
· Folha: é um nó sem filhos.
Árvore de busca binária (BST)
A árvore binária ocorre quando cada nó tem, no máximo, dois filhos. Neste tipo de árvore, caso ela tenha 0 ou 1 filho, o ponteiro para o lado sem filhos terá o valor null, sendo que os do lado esquerdo serão sempre menores que ele e os do lado direito, serão sempre maiores que ele.
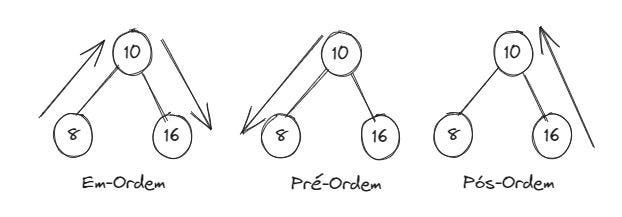
Em uma árvore binária ordenada (onde os elementos na árvore estão ordenados), para remover um elemento, precisamos verificar se o elemento a ser removido possui um filho ou não. Caso não possua, basta removê-lo da árvore. Mas, caso possua ramificações, precisamos trazer o elemento mais próximo do elemento que será removido (pois não podemos deixar em espaço vago). Para isso, precisamos percorrer a árvore (a partir do elemento removido) tudo para a esquerda e, depois, tudo para a direita. Existem três formas de se percorrer uma árvore binária:
Árvore AVL
Árvore AVL é uma árvore binária de busca balanceada, que tenta minimizar o número de comparações efetuadas no pior caso para uma busca. Contudo, para garantir essa propriedade, é preciso reconstruir a árvore para seu estado ideal a cada operação sobre seus nós (inclusão ou exclusão), o que causa um aumento no tempo computacional. Neste tipo de árvore, cada nó precisa de 2 bits de memória adicionais, o que acaba tomando mais espaço que a árvore rubro-negro (que falarei em seguida). O fator de balanceamento de um nó em uma árvore binária é a diferença de altura entre as subárvores da direita e da esquerda, dado pela fórmula: Fb = Hd − He
Onde Hd é a altura da subárvore à direito do nó e He é a altura da subárvore à esquerda, sendo que, a direita terá uma altura positiva e a esquerda terá uma altura negativa. Quanto maior for o fator de balanceamento, significa que a árvore está mais desbalanceada para a direita, e quanto mais negativo o fator de carga, mais desbalanceada para a esquerda a árvore está. Em uma árvore AVL, o fator de balanceamento de cada nó deve ficar entre 1 e -1. Exemplo:
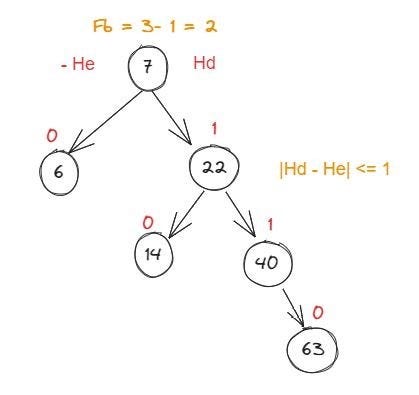
Como o nó folha é o último elemento, seu fator de balanceamento sempre será 0. Quando precisamos inserir um novo elemento, sempre vamos inseri-lo a partir de um nó folha, o que afetará o fator de balanceamento do seu elemento pai. Quando uma árvore AVL possui um fator de balanceamento maior que 2 ou menor que -2, precisamos realizar um desbalanceamento da árvore. Caso o fator de balanceamento seja menor que -2, precisamos fazer uma rotação para direita para balanceá-la. Vamos ver um exemplo:
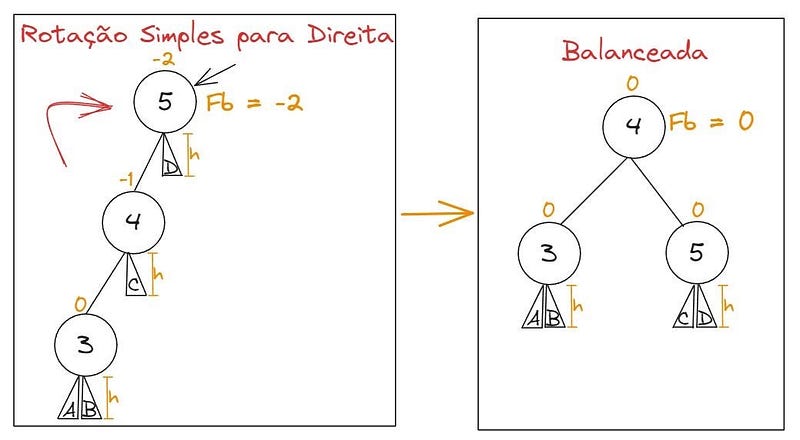
Caso o fator de balanceamento seja maior que 2, precisamos fazer uma rotação para esquerda, vide exemplo:
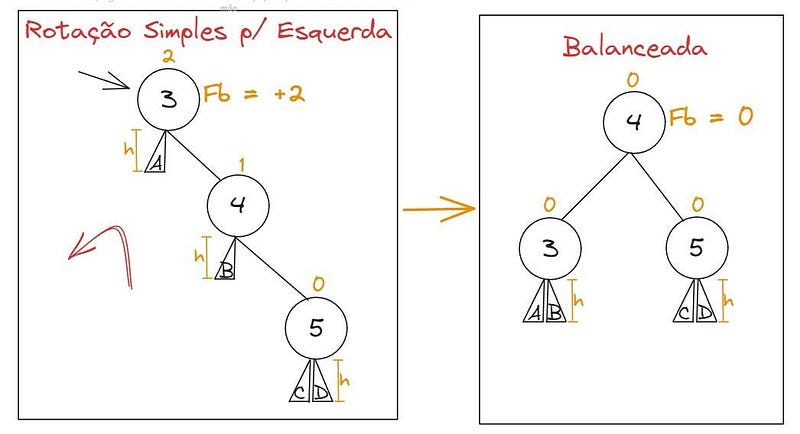
Dependendo do balanceamento da árvore, precisamos primeiro fazer uma rotação para direita, seguido de outra para a esquerda, para não ultrapassar o fator máximo de balanceamento. Exemplo:
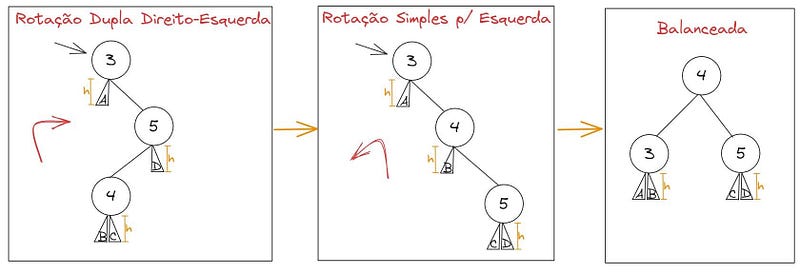
Em alguns casos, vamos precisar fazer primeiro uma rotação para a esquerda, depois outra para a direita. Exemplo:
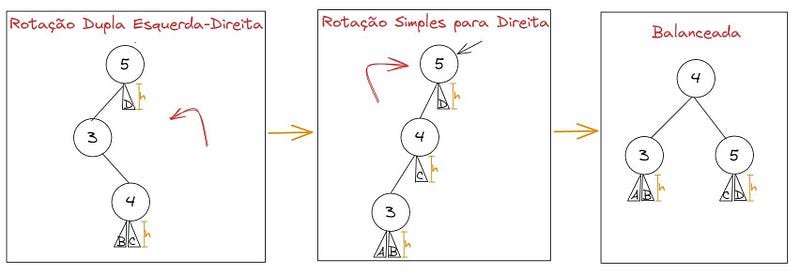
Árvore Rubro-Negra (RB Tree)
O node (nó) da árvore rubro-negra contém um campo extra de um bit que pode ser 0 ou 1 (representando a cor). O node raiz é sempre preto e, por padrão, todo node novo será da cor vermelha. Mas, depois de inserido na árvore, precisamos checar a cor do pai e dos filhos (pois um node vermelho só pode ter pais e filhos da cor preta). Se, depois de inserir um novo elemento, essa regra não estiver sendo seguida, precisamos repintar os nodes para rebalancear a árvore. Todo node no final da árvore (as folhas) que terminariam com os ponteiros sendo nulo, precisam apontar para um node de serviço chamado null node (isso é necessário para que eles sigam a regra de ordem das cores). Em uma representação gráfica, parece que temos vários null nodes no final, mas eles são apenas um ponteiro para um único null node (sendo representado dessa forma para uma melhor visibilidade da árvore, graficamente).
Se contarmos os nodes entre a raiz e o node nulo, deve sempre ter o mesmo número de nodes pretos (o que ocorre apenas se a árvore tiver a altura balanceada). Para balancearmos a árvore, precisamos fazer a rotação dos nós não-balanceados e, essa rotação, tem complexidade O(1) , independentemente do tamanho da árvore.
Neste tipo de árvore, precisamos de apenas um bit a mais de espaço extra para cada node, além dos ponteiros para o node nulo de cada folha. O tempo de inserção é um pouco mais alto, na ordem de grandeza de logaritmo, em comparação com a árvore desbalanceada. A busca nesse tipo de árvore é similar a árvore binária e, a remoção, é um pouco mais lenta, visto que é necessário checar se precisamos rebalancear a árvore após cada remoção. As árvores rubro-negras e as árvores AVLs têm o objetivo de chegar em uma árvore de procura binária, só que balanceada, oferecendo o menor tempo médio de procura binária.
Árvore B (B-Tree)
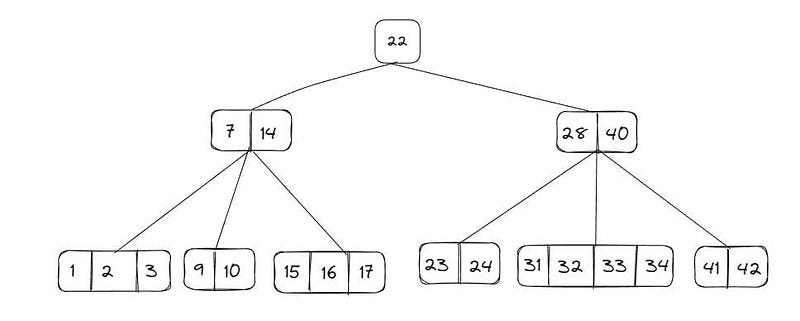
As árvores B são estruturas utilizadas para implementar tabelas de símbolos muito grandes, além de serem auto balanceadas. Ao contrário das árvores binárias que vimos anteriormente, nesse tipo de árvore os node podem ter n filhos. Essa estrutura é utilizada para armazenar grande quantidade de dados em disco e em memória secundária, sendo muito utilizada em banco de dados e em sistemas de arquivos, que manipulam grandes conjuntos de dados. Ela tenta equilibrar o custo de processamento com o custo de sistemas de busca e indexação, onde é utilizada para criar índices que permitem a recuperação rápida e eficiente de dados. Vejamos um exemplo:
Árvore B+ (B+ Tree)
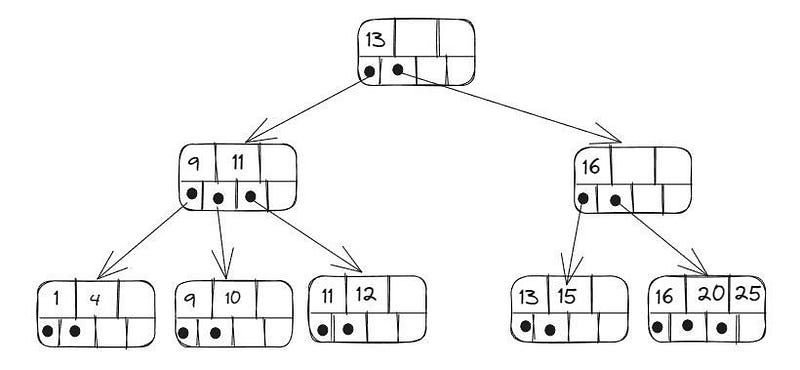
As árvores B+ (B plus tree) são um tipo de árvore B, onde os nodes não contêm os valores em sim, mas sim, apontam para os nós folhas, que contém os valores que queremos armazenar (os nós pais terão apenas as chaves que identificam esses valores). Esse tipo de árvore é utilizado em todos sistemas que utilizam armazenamento orientado a blocos, como no armazenamento de dados em disco, por exemplo. Vamos ver um exemplo:
Grafos
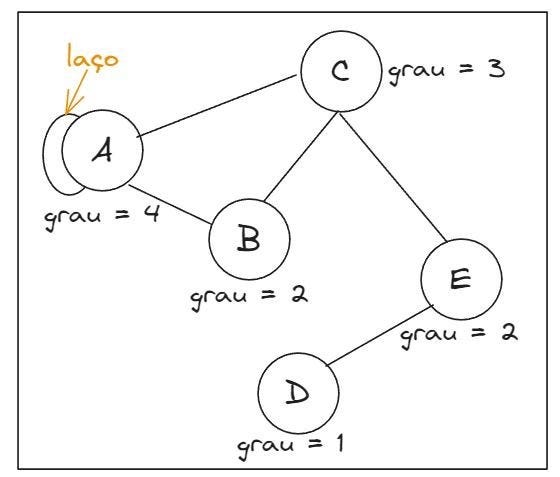
O grafo é uma estrutura de dados composta de vértices (ou nós) e arestas (ou arcos), em que cada aresta conecta dois vértices. Grafos sem laços ou arestas múltiplas (ou paralelas), são chamados de grafos simples. A ordem de um grafo é a quantidade de vértice que ele possui. O número de vezes que as arestas incidem sobre o vértice v é chamado de grau do vértice v, sendo que, o laço conta como dois graus. Exemplo:
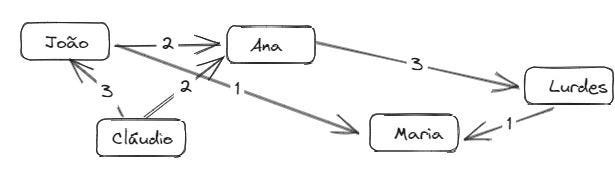
No grafo direcionado, as arestas possuem uma direção específica e, cada vértice terá um grau de entrada (quantidade de arestas que entram no vértice) e um grau de saída (quantidade de arestas que saem de um vértice). Um passeio (ou percurso) é uma sequência de arestas do tipo (V0, V1) ,(V1, V2) ,…,(VS − 1,VS) . Sendo que, V0 é o início do passeio e o V1 é o fim, e S é o comprimento de passeio:
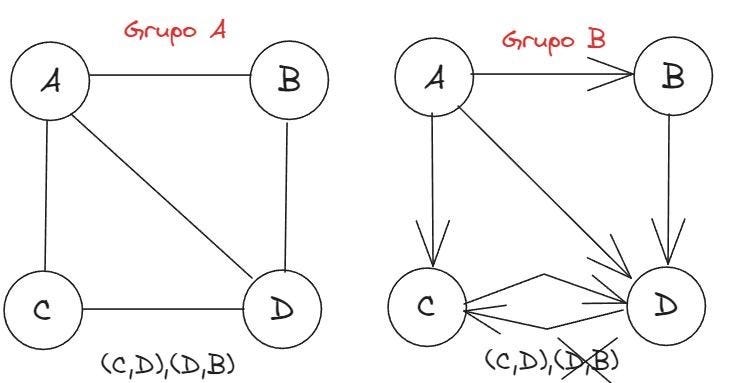
Já no grafo não-direcionado, não há uma direção específica para percorrê-lo. O grafo pode possuir um peso, que é um valor, seja na aresta ou no nó. O grafo é utilizado, por exemplo, para calcular a rota mais rápida entre dois pontos em um sistema de GPS, onde cada vértice/nó poderia representar as esquinas e as arestas seriam as ruas). As representações de um grafo podem ser:
1. Representação Gráfica: é representado através de pontos e linhas, como nas imagens acima;
2. Relação de Vértices e Arestas: é representado matematicamente como, por exemplo: V = {6A,6B,7A,7B};
3. Matriz de Adjacências: é representado por uma matriz, onde cada linha é representada por um vértice e, cada coluna, também vai representar um vértice. Quando um vértice se conectar a outro, vamos marcar o um naquela posição. Caso contrário, marcamos o 0. Vejamos um exemplo:
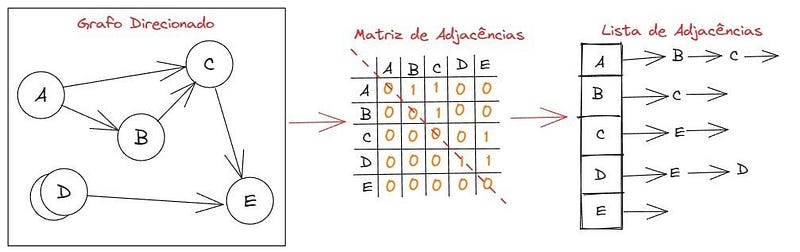
Caso a diagonal principal da matriz de adjacências só possua números 0, significa que o grafo não possui laços. E, caso o grafo possua arestas múltiplas, teremos valores maiores que um. Caso a matriz seja espelhada, ou seja, se a dividirmos em duas partes cortando pela diagonal principal e ambas as metades sejam iguais, indica que a matriz é simétrica e que estamos diante de uma matriz de adjacências simples de um grupo não direcionado. Além disso, nas linhas, temos o grau de saída e, na coluna, temos o grau de entrada.
4. Lista de Adjacências: ocorre quando criamos uma lista encadeada para cada um dos vértices de um grafo. Por exemplo, o vértice A têm arestas com o B e o C. Quando temos um laço, representamos chamando o vértice de forma recursiva, como no caso de D, que têm relação com E e com ele mesmo.
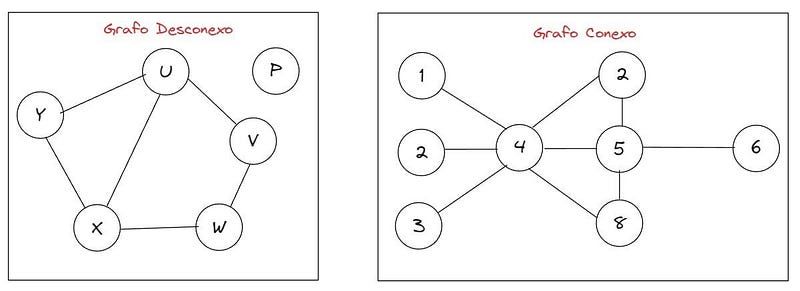
Um vértice de grau 0 é chamado de isolado e, um de grau 1, é chamado de pendente (ou folhas). O menor grau de um vértice em G é o grau mínimo, denotado δG, e o maior é o grau máximo, denotado Δ(G) . Um grupo é considerado conexo se existir um caminho entre qualquer par de vértices, caso contrário, ele é chamado de desconexo. Por fim, podemos dizer que dois vértices estão conectados se existe um caminho entre eles no grafo. Exemplo:
Busca (ou Pesquisa) em Largura
Para percorrer um grafo, precisamos definir primeiro o vértice. Em seguida, podemos utilizar a busca em largura ou a busca em profundidade para percorrê-lo. A busca em profundidade ocorre quando pegamos um vértice e vamos percorrendo os demais vértices, de acordo com a sequência do grafo. Já na busca em largura, buscamos apenas os vizinhos mais próximos daquele vértice e, quando não houver mais vizinhos, elegemos um novo vértice como centro das buscas e recomeçamos o processo, até percorrermos todos os elementos.
Algoritmo de Dijkstra
O algoritmo de Dijkstra é utilizado quando queremos encontrar o caminho mais rápido entre dois vértices, em um grafo com pesos (peso é um número associado a cada aresta deste grafo). Um grafo com pesos é chamado de grafo ponderado ou valorado, e um grafo sem pesos é chamado de grafo não ponderado ou não valorado. Um ponto importante é que esse algoritmo só vai funcionar se todos os pesos do grafo forem positivos. Se o grafo tiver pesos negativos, é necessário utilizar o algoritmo de Bellman-Ford. A complexidade de tempo em um caso geral é O(V²), onde V é o número de vértices. Esse algoritmo tem quatro passos:
1. Encontre o vértice mais “barato”. Esse é o vértice em que você consegue chegar no menor tempo possível;
2. Verifique se há um caminho mais barato para os vizinhos desse vértice. Caso exista, atualize os custos dele;
3. Repita até que você tenha feito isso para cada vértice do grafo;
4. Calcule o caminho final.
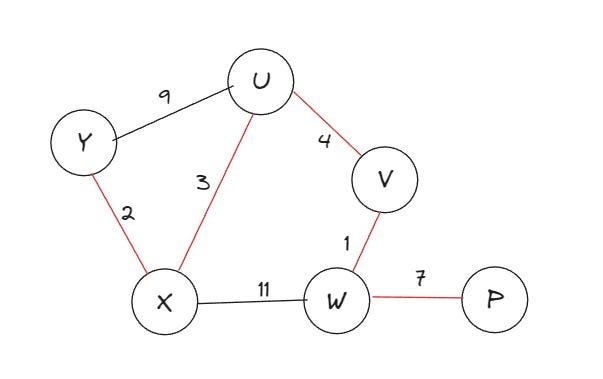
Vamos ver um exemplo de grafo em que podemos aplicar este algoritmo:
Algoritmo de Bellman-Ford
É um algoritmo que encontra o caminho mais curto em um grafo direcionado ponderado com pesos negativos, que funciona de forma similar ao algoritmo de Dijkstra. Ele começa definindo a distância de todos os vértices do grafo em relação ao vértice de origem como infinito, exceto para o vértice de origem, que é definido como 0. Em seguida, o algoritmo atualiza a distância de todos os vértices no grafo iterativamente, relaxando as arestas do grafo uma a uma, até que não haja mais atualizações a serem feitas. Este algoritmo é muito utilizado em redes de computadores (para calcular a rota mais curta em uma rede), sistema de transporte, rede de distribuição de energia, processamento de imagem, entre outros.
Algoritmos Gulosos
Os algoritmos gulosos são utilizados em problemas que não têm um algoritmo de solução rápidas (problemas NP-completo). Esses algoritmos enxergam apenas um passo de cada vez ao invés de se concentrar no todo, as duas premissas principal deste algoritmo são:
· Sempre procurar a solução ideal em um dado passo;
· E executar o passo.
Os problemas NP-completos são problemas complexos e de difícil resolução, onde não existe um algoritmo que consiga resolvê-lo de forma rápida. Um exemplo é o problema do caixeiro-viajante, que falarei a seguir.
Problema do Caixeiro-Viajante (Traveling Salesman)
Suponha que um caixeiro viajante tenha de visitar n cidades diferentes, iniciando e encerrando sua viagem na primeira cidade. Suponha, também, que não importa a ordem com que as cidades são visitadas e que de cada uma delas pode-se ir diretamente a qualquer outra. O problema do caixeiro viajante consiste em descobrir a rota que torna mínima a viagem total. Se ele precisar percorrer três cidades, precisamos de apenas seis operações para descobrir qual a melhor rota. Mas se tivermos cinco cidades, seriam necessárias 120 operações, e se fossem 8 cidades, seriam necessárias 40430 operações para calcularmos a melhor rota!
Podemos ver que, à medida que a quantidade de cidades a se percorrer sobe, as operações sobem de forma exponencial, inviabilizando o cálculo da rota em um problema que possua com centenas ou milhares de cidades. Por conta disso, esse problema tem uma performance de O(n!). Vamos ver como ficaria um exemplo de rotas ao passar por determinadas cidades nos Estados Unidos:
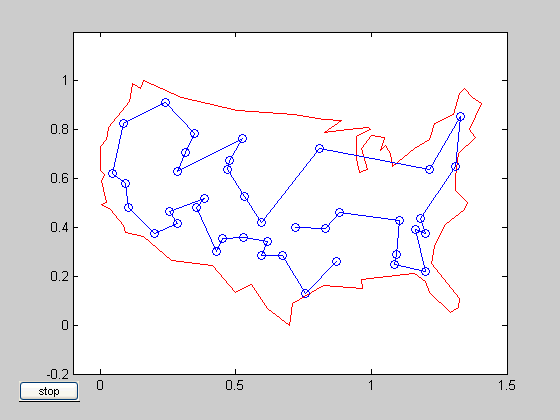
Fonte: https://nature.berkeley.edu/getz/dominance/GA/gads/gadsdemos/html/traveling_salesman_demo.html
K-Vizinhos mais próximos (KNN)
O algoritmo dos k-vizinhos mais próximos é utilizado na classificação (classificar em grupo) e também na regressão (adivinhar uma resposta, como um número). Este algoritmo tenta classificar cada amostra de um conjunto de dados avaliando sua distância em relação aos vizinhos mais próximos. Se os vizinhos mais próximos forem majoritariamente de uma classe, a amostra em questão será classificada nesta categoria. Ao trabalhar com esse algoritmo, é muito importante saber escolher as características certas para serem comparadas, que são:
· Características diretamente correlacionados aos objetos que você está tentando recomendar (como filmes, por exemplo);
· Características imparciais (por exemplo, se as únicas opções fornecidas aos usuários forem séries de drama, esta avaliação não fornecerá nenhuma informação útil em relação a animes).
Este algoritmo é muito utilizado em sistemas de recomendações como, por exemplo, em plataformas de streaming de vídeo e aprendizado de máquina. Exemplo:
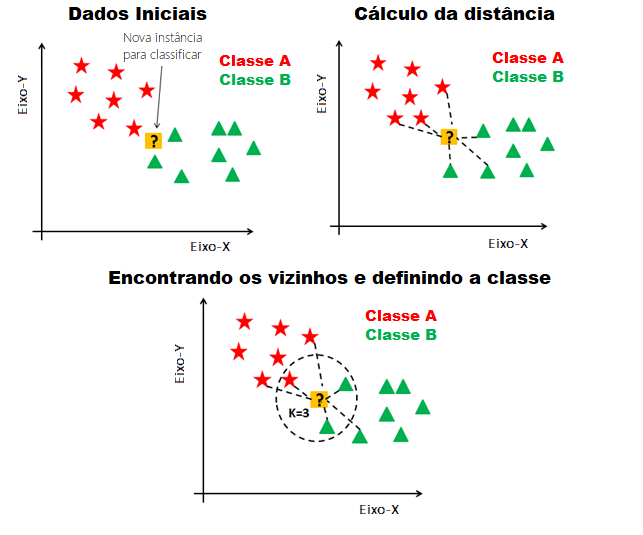
Fonte: https://medium.com/@msremigio/aprendizagem-baseada-em-inst%C3%A2ncias-knn-7e2c6f0778bc
Conclusão
Estrutura de Dados é um assunto complexo, que todo programador acaba tendo contato em algum momento da sua carreira. Este artigo cobriu apenas os conceitos básicos de algoritmos e estruturas de dados. Dito isto, pretendo trazer a implementação de algumas dessas estruturas de dados em Java ou Kotlin, para alinhar a teoria e prática, em artigos futuros. Quase todas as imagens deste artigo foram desenhadas por mim, utilizando a ferramenta Excalidraw e as imagens e o gif que peguei da internet estão referenciados na próxima legenda. Fiquem à vontade para comentarem sobre eventuais erros que encontrarem neste artigo ou apenas para opinarem.
Referências Utilizadas
Livro Entendendo Algoritmos: Um Guia Ilustrado Para Programadores e Outros Curiosos — Autor Aditya Y. Bhargava
Livro Estruturas de Dados e Seus Algoritmos — Autores Jayme Luiz Szwarcfiter e Lilian Markenzon
Artigo Tabelas Hash — Autor João Arthur Brunet — Link: https://joaoarthurbm.github.io/eda/posts/hashtable/
Artigo O que é e como funciona o algoritmo KNN? — Link: https://didatica.tech/o-que-e-e-como-funciona-o-algoritmo-knn/
Artigo Tudo o que você precisa saber sobre estruturas de dados em árvore — Autor TK — Link:
Artigo Aprendizagem Baseada em Instâncias KNN — Autor Matheus Remigio — Link: https://medium.com/@msremigio/aprendizagem-baseada-em-inst%C3%A2ncias-knn-7e2c6f0778bc
Canal Fábio Akita — O que vem DEPOIS do Hello World | Consertando meu C — https://www.youtube.com/watch?v=9GdesxWtOgs&ab_channel=FabioAkita
Canal Fábio Akita — Hello World Como Você Nunca Viu! | Entendendo C — https://www.youtube.com/watch? v=9GdesxWtOgs&ab_channel=FabioAkita
Canal Fábio Akita — Árvores: O Começo de TUDO | Estruturas de Dados e Algoritmos — https://www.youtube.com/watch? v=9GdesxWtOgs&list=RDCMUCib793mnUOhWymCh2VJKplQ&index=12&ab_channel=FabioAkita
Canal Professor Douglas Maioli — Playlist Estrutura de Dados — https://www.youtube.com/watch?v=twvgnfOnVQ&list=PLrOyM49ctTx_AMgNGQaic10qQJpTpXfn_&index=1&ab_channel=ProfessorDouglasMaioli
Canal Professor Douglas Maioli — Playlist de Teoria de Grafos — https://www.youtube.com/watch?v=T6yKp82k9vM&list=PLrOyM49ctTxxtyVeuO7ylclgXHd4ws9a&index=2&ab_channel=ProfessorDouglasMaiol Canal 2Guarinos — Playlist Estrutura de Dados com Java — https://www.youtube.com/watch? v=8zVdz6TyV_c&list=PLTLAlheiUm5FRR5BNn4iBFwzYHiNq2Iv2&ab_channel=2Guarinos
Canal Loiane Groner — Playlist Curso Estrutura de Dados e Algoritmos Java — https://www.youtube.com/watch?v=N3K8PjFOhy4&list=PLGxZ4Rq3BOBrgumpzzl8kFMw2DLERdxi&ab_channel=LoianeGroner








