<Direto ao Ponto 58> Algoritmos de Ordenação
- #Informática Básica

Artigos desta série: ( < ) Anterior | Índice | Seguinte ( > )
Olá, dev!
Este é mais um artigo da série DIRETO AO PONTO, que eu estou escrevendo para a DIO. Ele vai tratar dos algoritmos de ordenação.
Sumário
1. Introdução
2. Os algoritmos de ordenação
3. Complexidade dos algoritmos de ordenação
4. Considerações finais
5. Referências
1 – Introdução
Eu criei a série de artigos DIRETO AO PONTO com o objetivo de apresentar, de forma simples e direta, conhecimentos básicos da programação e de computação, principalmente, para os iniciantes.
Aqui, são tratados temas como lógica de programação, linguagens, hardware dos computadores, história da computação e assuntos relacionados à plataforma da DIO, como a escrita de artigos e os desafios de código.
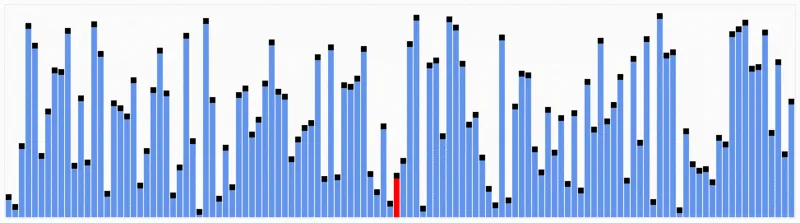
Neste artigo, serão tratados os algoritmos de ordenação (OBS: A figura da capa deste artigo é uma ordenação de valores pelo método Quick Sort)
Também chamados de algoritmos de classificação, junto com os algoritmos de busca, eles são usados por muitos programas, com o objetivo de tornar mais eficientes as operações de busca ou permitir uma filtragem mais rápida de dados.
Existem vários algoritmos disponíveis, cada um com suas características próprias, alguns mais adequados para determinados tipos de aplicações do que outros.
Além disso, eles pertencem a diferentes tipos de complexidade. Para uma aplicação específica, entre vários algoritmos possíveis para a implementação, é importante escolher aquele com menor complexidade de tempo ou de espaço de memória.
2 – Os algoritmos de ordenação
Os algoritmos de ordenação são técnicas utilizadas para organizar uma lista de elementos em uma determinada ordem (geralmente crescente ou decrescente).
Existem vários tipos de algoritmos de ordenação, cada um com suas características, vantagens e desvantagens.
A seguir, são mostrados alguns dos principais algoritmos de ordenação, sua complexidade e aplicação:
Bubble Sort - Compara pares de elementos adjacentes e os troca se estiverem na ordem errada. Este processo é repetido várias vezes até que a lista esteja ordenada. Sua complexidade é O(n²).
Como funciona?
Em cada passo, movendo-se da esquerda para a direita, os elementos adjacentes são trocados, se necessário, e colocados em ordem crescente. Cada passo move o próximo maior elemento para a sua posição final (marcada em verde).
O primeiro passo leva o maior elemento para a última posição, o segundo leva o maior elemento dos que restaram para a penúltima posição e assim por diante. A figura abaixo mostra a dinâmica seguida para o primeiro passo:

Exemplo em Python:
def bubble_sort(arr):
n = len(arr)
for i in range(n):
for j in range(0, n-i-1):
if arr[j] > arr[j+1]:
arr[j], arr[j+1] = arr[j+1], arr[j]
arr = [30,50,40,20,10]
print(arr)
bubble_sort(arr)
print(arr)
Selection Sort - Encontra o menor elemento da lista e o coloca na primeira posição. Em seguida, repete o processo para o restante da lista. Sua complexidade também é O(n²).
Como funciona?
Para cada passo, movendo-se da esquerda para a direita, procura-se o próximo maior valor. Cada elemento maior é marcado como o novo maior. Encontrado o maior de todos, ele é trocado com outro elemento para a sua posição final (e é marcado com uma cor diferente – verde).
O primeiro passo leva o maior elemento para a última posição, o segundo leva o maior elemento dos que restaram para a penúltima posição e assim por diante. A figura abaixo mostra a dinâmica seguida para o primeiro passo:

Exemplo em Python:
def selection_sort(arr):
n = len(arr)
for i in range(n):
min_idx = i
for j in range(i+1, n):
if arr[j] < arr[min_idx]:
min_idx = j
arr[i], arr[min_idx] = arr[min_idx], arr[i]
arr = [30,50,40,20,10]
print(arr)
selection_sort(arr)
print(arr)
Insertion Sort - Percorre a lista, insere cada elemento na posição correta em uma sublista crescente. Tem complexidade O(n²).
Como funciona?
Os elementos à esquerda (em verde) são considerados ordenados. No início, considera-se ordenado o elemento da posição 0. Move-se o elemento da posição 1 (em laranja) para a esquerda, se necessário, até que ele esteja na posição correta.
Depois, faz o mesmo com o elemento da posição 2 e assim por diante.
A figura abaixo mostra a dinâmica seguida até o penúltimo passo, faltando apenas processar o último elemento da lista (10):

Exemplo em Python:
def insertion_sort(arr):
for i in range(1, len(arr)):
key = arr[i]
j = i - 1
while j >= 0 and key < arr[j]:
arr[j + 1] = arr[j]
j -= 1
arr[j + 1] = key
arr = [30,40,50,20,10]
print(arr)
insertion_sort(arr)
print(arr)
Merge Sort - Algoritmo de divisão e conquista que divide a lista em duas sublistas, ordena-as e depois as combina. Boa complexidade de O(n log n).
Como funciona?
Primeiro, divida a lista original em novas sublistas com o mesmo número de elementos ou o mais próximo disso.
Para cada sublista, faça o mesmo, subdividindo-o até que só haja sublistas com apenas 2 elementos ou unitários (com apenas 1 elemento).
Nas sublistas com 2 elementos, caso eles estejam em ordem decrescente, troque os valores.

Após a troca dos elementos nas sublistas da parte de baixo, selecione o menor valor entre os primeiros elementos (30 e 50) de cada uma das 2 sublistas da esquerda, inserindo-o (30) como o primeiro valor da sublista superior a eles, repetindo o processo até preencher a sublista acima deles (30, 50, 60).

Concluindo este passo:

Finalmente, chegamos à sublista original ordenada:

Exemplo em Python:
def merge_sort(arr):
if len(arr) > 1:
mid = len(arr) // 2
L = arr[:mid]
R = arr[mid:]
merge_sort(L)
merge_sort(R)
i = j = k = 0
while i < len(L) and j < len(R):
if L[i] < R[j]:
arr[k] = L[i]
i += 1
else:
arr[k] = R[j]
j += 1
k += 1
while i < len(L):
arr[k] = L[i]
i += 1
k += 1
while j < len(R):
arr[k] = R[j]
j += 1
k += 1
arr = [60,30,50,40,20,10]
print(arr)
merge_sort(arr)
print(arr)
Quick Sort – Algoritmo baseado no princípio de divisão e conquista. A técnica se baseia na seleção de um pivô e particionamento da lista original de elementos em dois subgrupos, com os menores que o pivô de um lado e os maiores do outro. Em seguida, as sublistas são ordenadas recursivamente. Sua complexidade é O(n log n) para o melhor caso e O(n²) no pior caso. (OBS: A figura da capa deste artigo é uma ordenação de valores pelo método Quick Sort)
Como funciona?
Primeiro, selecione um pivô (elemento base que dividirá os outros elementos da lista original.
Passe todos os elementos menores que o pivô para a esquerda do pivô, na mesma ordem em que estão na lista original. Passe todos os elementos maiores que o pivô para a direita dele, na mesma ordem em que estão na lista. Este processo se chama particionamento.
Recursivamente, repita este mesmo processo para as sublistas formados à esquerda e à direita do pivô, até que se chegue a sublistas com 1 ou zero elemento (ver figura abaixo).

Cada sublista que contenha apenas 1 elemento já está ordenada. Aí, é só retornar para as sublistas superiores com a ordenação correta de cada sublista esquerda ou direita até a lista original, que estará ordenada.
Finalmente, junte todos os elementos das sublistas dos passos anteriores e os pivôs, nas posições corretas, para preencher a lista original (ver figura abaixo).

Exemplo em Python:
def quick_sort(arr):
if len(arr) <= 1:
return arr
else:
pivot = arr[len(arr) // 2]
left = [x for x in arr if x < pivot]
middle = [x for x in arr if x == pivot]
right = [x for x in arr if x > pivot]
return quick_sort(left) + middle + quick_sort(right)
arr = [60,30,50,40,70,20,10]
print(arr)
arr = quick_sort(arr)
print(arr)
3 – Complexidade dos algoritmos de ordenação
O gráfico a seguir mostra a complexidade dos algoritmos de ordenação tratados neste artigo:

Já a tabela abaixo compara a complexidade de cada algoritmo tratado aqui para o melhor caso e pior caso de cada um deles:

Em resumo, os algoritmos de ordenação têm diferentes características que os tornam mais adequados para diferentes situações. Para listas pequenas ou quase ordenadas, algoritmos simples como o Insertion Sort podem ser mais eficientes. Para listas grandes, Merge Sort e Quick Sort são os mais usados devido à sua eficiência no caso médio.
4 – Considerações finais
Este é mais um artigo da série DIRETO AO PONTO, que eu estou escrevendo para a DIO.
Desta vez, foram apresentados os algoritmos de ordenação, também chamados de algoritmos de classificação.
Eles são muito usados na programação e tem como objetivo tornar mais eficientes as operações de busca ou permitir uma filtragem mais rápida de dados.
Existem vários algoritmos disponíveis, cada um mais adequados para determinados tipos de aplicações do que outros.
Cada algoritmo apresenta um nível de complexidade, que é uma medida da eficiência dele em termos de tempo de execução e uso de memória. A complexidade de um algoritmo é muito importante para entender como ele se comporta à medida que o tamanho da entrada aumenta, principalmente nestes tempos de uso de volumes de dados enormes, em aplicações Ciência de Dados e de IA.
Neste artigo foram mostrados alguns dos principais algoritmos de ordenação, seus funcionamentos, ilustração da evolução do método e exemplos de uso na linguagem Python.
Além disso, foram mostrados dados comparativos da evolução deles com o aumento do número de dados de entrada.
Em resumo, se você tiver que escolher um algoritmo de ordenação para uma aplicação específica, entre vários algoritmos possíveis para a implementação, é melhor escolher aquele com menor complexidade de tempo ou de espaço de memória, pois ele será mais eficiente.
O próximo artigo tratará de algoritmos de busca, parentes próximos dos algoritmos de ordenação.
5 – Referências
Praticamente todo o conteúdo deste artigo foi tirado do que eu aprendi (e me lembro) sobre o assunto desde o início da minha carreira como programador, desde os anos 80 até agora.
Os códigos em Python foram consultados no ChatGPT. Depois, eles foram atualizados por mim e foram executados com sucesso.
Artigos desta série: ( < ) Anterior | Índice | Seguinte ( > )