<Direto ao Ponto 57> Complexidade de algoritmos
- #Informática Básica
Artigos desta série: ( < ) Anterior | Índice | Seguinte ( > )
Olá, dev!
Este é mais um artigo da série DIRETO AO PONTO, que eu estou escrevendo para a DIO. Ele vai tratar da complexidade de algoritmos, um tema que trata da eficiência dos algoritmos que usamos nos nossos programas.
ATENÇÃO: Estou tendo problemas para editar os códigos deste artigo. Quando eu conseguir editá-los, removo esta mensagem.
Sumário
1. Introdução
2. Os algoritmos computacionais
3. Complexidade de algoritmos
4. Considerações finais
5. Referências
1 – Introdução
Eu criei a série de artigos DIRETO AO PONTO com o objetivo de apresentar, de forma simples e direta, conhecimentos básicos da programação e de computação, principalmente, para os iniciantes.
Aqui, são tratados temas como lógica de programação, linguagens, hardware dos computadores, história da computação e assuntos relacionados à plataforma da DIO, como a escrita de artigos e os desafios de código.
Neste artigo, vou tratar da tratar da complexidade de algoritmos, um tema que trata da eficiência dos algoritmos que usamos nos nossos programas.
Afinal, programar é codificar algoritmos.
Mas será que nós escolhemos os melhores algoritmos? Ou codificamos usando o primeiro que lembramos que resolve nosso problema.
Vamos ver o que isso significa!
2 – Os algoritmos computacionais
Um algoritmo é a execução de uma sequência ordenada de ações para resolver um problema ou realizar uma tarefa específica.
Eles não são usados apenas na programação, mas até em tarefas do nosso cotidiano, como trocar uma lâmpada, um pneu, instalar um equipamento novo, ou até para fazer um bolo, por exemplo.
Para fazer um bolo seguindo uma receita pegamos os ingredientes, depois seguimos determinados passos para fazer a massa, depois colocar no forno, esperar um tempo e tirar o bolo pronto, que é o resultado esperado.
Se a ordem ou a duração de uma das ações da receita for alterada, pode ser que o bolo não fique bom.
E para fazer 50 bolos, será que é só seguir a mesma receita 50 vezes uma atrás da outra? Ou teria alguma solução melhor, mais rápida, como usar mais de 1 pessoa e de 1 forno, por exemplo?
A eficiência da aplicação de um algoritmo para ter sucesso em uma loja de bolos é importante para o negócio. Como fazer mais bolos com a mesma qualidade e em menos tempo?
Na programação é a mesma coisa. Programar é codificar algoritmos. As instruções são escritas em uma linguagem de programação e, quando executadas pelo computador, produzem um resultado desejado.
Além de computação, os algoritmos também são usados em muitas áreas, como engenharia, matemática e negócios, por exemplo.
Os algoritmos são a base da programação e são usados em praticamente todos os aspectos do desenvolvimento de software. Eles são usados para criar programas que realizam tarefas específicas, como processamento de dados, tomada de decisão, busca e ordenação. Algoritmos também são usados para otimizar o desempenho de programas e torná-los mais eficientes.
Existem muitos tipos diferentes de algoritmos, cada um com suas próprias características e usos, por exemplo:
· Algoritmos de busca: usados para encontrar um item específico em uma coleção de dados;
· Algoritmos de ordenação: usados para classificar uma coleção de dados;
· Algoritmos de compressão: usados para reduzir o tamanho de arquivos de dados;
· Algoritmos de criptografia: usados para proteger a privacidade e a segurança de dados.
No entanto, a escolha do algoritmo certo é crucial para garantir que um programa funcione corretamente e de forma eficiente. Para escolher o algoritmo certo, é importante entender as necessidades do programa e os dados com os quais ele trabalhará. Também é importante considerar fatores como a eficiência e a escalabilidade do algoritmo, por exemplo.
Cada algoritmo tem aplicações específicas e pode ser adaptado para resolver uma variedade de problemas.
3 – Complexidade de Algoritmos
A complexidade de algoritmos é uma medida que avalia a eficiência de um algoritmo em termos de tempo de execução e uso de memória. Ela é fundamental para entender como um algoritmo se comporta à medida que o tamanho da entrada aumenta, ajudando a escolher a solução mais adequada para um problema específico.
A análise da complexidade de algoritmos é crucial para o desenvolvimento de soluções eficientes e escaláveis. Compreender os diferentes tipos de complexidade ajuda a escolher o algoritmo mais adequado para cada situação, garantindo um desempenho otimizado.
· Complexidade de Tempo: Refere-se ao tempo necessário para executar um algoritmo. É geralmente expressa em termos de notação Big-O (Lê-se Bigue Ou), que descreve o comportamento assintótico do algoritmo;
· Complexidade de Espaço: Refere-se à quantidade de memória necessária para executar um algoritmo. Ela também é expressa em termos de notação Big-O.
A escolha de um algoritmo para resolver um determinado problema deve levar em conta:
· Eficiência: Algoritmos eficientes são essenciais para lidar com grandes volumes de dados e garantir que os programas sejam rápidos e responsivos;
· Escalabilidade: A análise da complexidade ajuda a prever como um algoritmo se comportará à medida que o tamanho da entrada cresce, permitindo a escolha de soluções escaláveis;
· Comparação: Comparar diferentes algoritmos que resolvem o mesmo problema ajuda a selecionar o mais adequado.
Os algoritmos podem apresentar os seguintes tipos de complexidade:
Constante O(1): O tempo de execução não depende do tamanho da entrada. Exemplo: Acessar um elemento em um array por índice.
Exemplo de implementação, em Python:
def get_first_element(arr):
return arr[0]
Linear O(n): O tempo de execução cresce linearmente com o tamanho da entrada. Exemplo: Percorrer todos os elementos de uma lista.
Exemplo:
def print_elements(arr):
for element in arr:
print(element)
Logarítmica O(log n): O tempo de execução cresce logaritmicamente com o tamanho da entrada. Exemplo: Busca binária.
Exemplo:
def binary_search(arr, target):
left, right = 0, len(arr) - 1
while left <= right:
mid = (left + right) // 2
if arr[mid] == target:
return mid
elif arr[mid] < target:
left = mid + 1
else:
right = mid - 1
return -1
Quadrática O(n2): O tempo de execução cresce quadraticamente com o tamanho da entrada. Exemplo: Ordenação por inserção.
Exemplo:
def insertion_sort(arr):
for i in range(1, len(arr)):
key = arr[i]
j = i - 1
while j >= 0 and key < arr[j]:
arr[j + 1] = arr[j]
j -= 1
arr[j + 1] = key
Exponencial O(2n): O tempo de execução cresce exponencialmente com o tamanho da entrada. Exemplo: Problemas de Recursividade, como a sequência de Fibonacci.
Exemplo:
def fibonacci(n):
if n <= 1:
return n
else:
return fibonacci(n-1) + fibonacci(n-2)
Fatorial O(n!): O tempo de execução cresce fatorialmente com o tamanho da entrada. Exemplo: Algoritmo de permutação.
Exemplo:
def permute(arr):
if len(arr) == 0:
return [[]]
result = []
for i in range(len(arr)):
rest = arr[:i] + arr[i+1:]
for p in permute(rest):
result.append([arr[i]] + p)
return result
O(n!): O tempo de execução cresce linearmente, mas multiplicado por um fator logarítmico, com o tamanho da entrada. Exemplo: Ordenação por Merge Sort.
Exemplo:
def merge(arr, left, mid, right):
n1 = mid - left + 1
n2 = right - mid
L = arr[left:mid + 1]
R = arr[mid + 1:right + 1]
i = 0 # índice para sublista L
j = 0 # índice para sublista R
k = left # índice para a lista original
# Intercalando as duas sublistas
while i < n1 and j < n2:
if L[i] <= R[j]:
arr[k] = L[i]
i += 1
else:
arr[k] = R[j]
j += 1
k += 1
while i < n1:
arr[k] = L[i]
i += 1
k += 1
while j < n2:
arr[k] = R[j]
j += 1
k += 1
def merge_sort(arr, left, right):
if left < right:
mid = (left + right) // 2
# Ordenar a primeira e a segunda metade
merge_sort(arr, left, mid)
merge_sort(arr, mid + 1, right)
# Intercalar as duas metades ordenadas
merge(arr, left, mid, right)
# Exemplo de uso
arr = [38, 27, 43, 3, 9, 82, 10]
print("Array original:", arr)
merge_sort(arr, 0, len(arr) - 1)
print("Array ordenado:", arr)
Cúbica O(n3): O tempo de execução cresce cubicamente com o tamanho da entrada. Exemplo: Multiplicação de Matrizes pelo método tradicional.
Exemplo:
def multiplicar_matrizes(A, B):
linhas_A = len(A)
colunas_A = len(A[0])
linhas_B = len(B)
colunas_B = len(B[0])
if colunas_A != linhas_B:
raise ValueError("O número de colunas de A deve ser igual ao número de linhas de B.")
resultado = [[0 for _ in range(colunas_B)] for _ in range(linhas_A)]
# Multiplicação de matrizes
for i in range(linhas_A):
for j in range(colunas_B):
for k in range(colunas_A):
resultado[i][j] += A[i][k] * B[k][j]
return resultado
# Exemplo de uso
A = [
[1, 2, 3],
[4, 5, 6]
]
B = [
[7, 8],
[9, 10],
[11, 12]
]
resultado = multiplicar_matrizes(A, B)
print("Matriz resultante:")
for linha in resultado:
print(linha)
Só para dar uma ideia de grandeza, veja os valores relativos ao número de itens usados em um algoritmo de cada tipo citado acima e os tempos associados à sua execução.

OBS: O crescimento do tempo para um algoritmo de complexidade fatorial O(n!) é tão absurdo, fora da escala dos números mostrados acima, que nem entrou nesta tabela. Por exemplo, 8! dá 40 mil, já 128! É aproximadamente 1,3 x 1089.
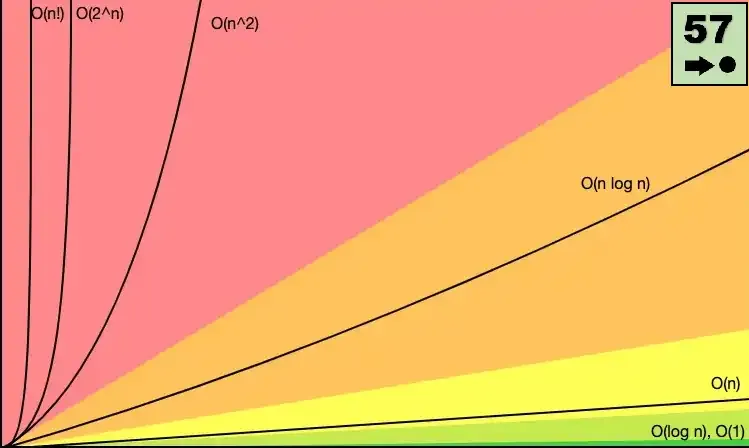
Para ilustrar os comportamentos destes tipos de algoritmos e destes números, veja o gráfico a seguir:

4 – Considerações finais
Este é mais um artigo da série DIRETO AO PONTO, que eu estou escrevendo para a DIO.
Desta vez, foi apresentada complexidade de algoritmos. Eles são a base da programação e são usados em todos os códigos que criamos.
Primeiro, foi descrito o que é um algoritmo, tanto de uso cotidiano quanto computacional.
Depois, foram apresentados os principais tipos de algoritmos, em relação à sua complexidade do tempo de execução, com exemplos de códigos.
Por fim, foi apresentada uma comparação do crescimento do tempo de execução entre os algoritmos de cada um dos tipos de complexidades tratados aqui, tanto numericamente quanto graficamente.
Cada problema tem várias maneiras de ser resolvido, cada uma com sua própria complexidade.
É responsabilidade do programador buscar melhores algoritmos para implementar soluções com mais eficiência.
Se existem várias soluções diferentes para resolver um problema, escolha um algoritmo que tem menor complexidade para implementar seu código.
Nesta época de Big Data e IA, muitas vezes precisamos trabalhar com enormes quantidades de dados e um algoritmo de melhor complexidade sempre será a solução mais eficiente.
Nos próximos artigos, eu ainda vou continuar falando de complexidade de algoritmos, mas de algoritmos específicos, de ordenação e busca.
5 – Referências
Praticamente todo o conteúdo deste artigo foi tirado do que eu aprendi (e me lembro) sobre o assunto desde o início da minha carreira como programador, desde os anos 80 até agora.
Para detalhar os tipos de complexidade com exemplos atuais de aplicação, bem como para codificar alguns exemplos, eu me atualizei com uma consulta ao ChatGPT.
Artigos desta série: ( < ) Anterior | Índice | Seguinte ( > )