<Direto ao Ponto 17> Representação de dados em binário

Artigos desta série: ( < ) Anterior | Índice | Seguinte ( > )

Olá, dev!

Este é mais um artigo da série DIRETO AO PONTO, que eu estou escrevendo para a DIO. Ele vai tratar da representação de dados em binário, para que eles possam ser usados pelo computador na execução dos programas.

Sumário

1.   Introdução

2.   Resumo do sistema binário

3.   Representação de dados em binário

4.   Considerações finais

5.   Referências

1 – Introdução

A série DIRETO AO PONTO enfoca artigos sobre conhecimentos básicos da programação e é voltada, principalmente, para os iniciantes.

Este novo artigo vai tratar da representação de dados em binário, para que eles possam ser usados pelo computador na execução dos programas.

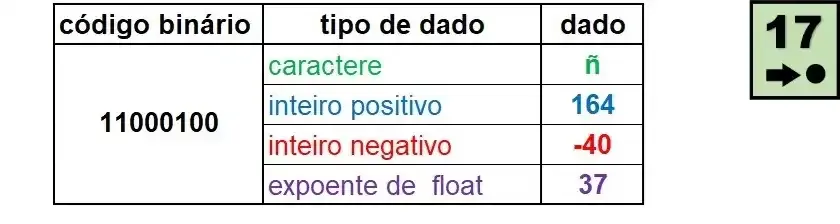
Na capa deste artigo, é mostrado um único código binário armazenado na memória de um computador e ele pode representar 4 dados diferentes, dependo do tipo de representação escolhido, um para cada tipo de dado diferente.

2 – Resumo do sistema de numeração binário

Eu já publiquei alguns artigos desta série que tratavam dos detalhes dos sistemas de numeração (incluindo o sistema binário e o hexadecimal), portanto, aqui será apresentado apenas um resumo do que eu considero importante como base para o conteúdo deste artigo que você lê agora.

O sistema binário é um tipo de representação de números que usa a base 2, de forma semelhante ao sistema decimal, que usa a base 10.

Como no sistema decimal, a forma de representar as quantidades também é baseada na notação posicional, em que um algarismo vale uma quantidade diferente de acordo com a posição que ele ocupa dentro do número.

Um número é dividido em diversas ordens, cada uma associada a uma potência do número da base. Desta forma, é possível decompor um número decimal em potências de 10, cada uma delas representando uma das ordens do número.

Por exemplo, na base 10, o número 2325 pode ser representado pelas potências de 10 seguintes:

2325 =

2000 + 300 + 20 + 5 =

2 x 1000 + 3 x 100 + 2 x 10 + 5 x 1 =

2 x 10³ + 3 x 10² + 2 x 10¹ + 5 x 10⁰

Resumindo, 2 milhares, 3 centenas, 2 dezenas e 5 unidades.

Veja que o algarismo 2 mais à direita não vale só 2 unidades, mas 20 unidades, pois está na ordem das dezenas. Já o algarismo 2 mais à esquerda vale 2000 unidades, e assim por diante. Assim funciona uma notação posicional.

A diferença básica entre o sistema decimal e o sistema binário é a base, 10 no decimal, enquanto no binário, a base é 2.

Por exemplo, o número decimal 107 pode ser representado em binário como 01101011, e pelas quantidades e potências de 2 seguintes:

0 x128 + 1 x 64 + 1 x 32 + 0 x 16 + 1 x 8 + 0 x 4 + 1 x 2 + 1 x 1 = 

0 x 2⁷ + 1 x 2⁶ + 1 x 2⁵ + 0 x 2⁴ + 1 x 2³ + 0 x 2² + 1 x 2¹ + 1 x 2⁰ =

Em geral, um número binário é representado com um 0b antes dos seus algarismos, um hexadecimal, com um 0x.

Números fracionários

Até aqui, só lidamos com números inteiros positivos, mas as quantidades decimais fracionárias também podem ser representadas por potências de 2 negativas:

Por exemplo, o número decimal 3,75 pode ser decomposto nas partes:

·        Parte Inteira: 3 = 1 x 2¹ + 1 x 2⁰ = 11 em binário (00000011, com 8 bits);

·        Parte fracionária 0,75 = 0,5 + 0,25 = 1 x 2^-1 + 1 x 2^-2 = 0.11 em binário.

Juntando as 2 partes, o número 3,75 é representado pelo binário 11,11.

Os zeros á esquerda do primeiro algarismo significativo não alteram o valor do número, bem como aqueles à direita do último algarismo significativo.

Para qualquer número decimal, podemos encontrar os bits da parte fracionária multiplicando-a por 2 e registrando cada 0 ou 1 da parte inteira resultante, repetindo o processo para quantos bits desejarmos armazenar.

Por exemplo, para o número decimal fracionário 0,361, vamos registrar 4 bits binários:

0,361 x 2 = 0,722 -> registra a parte inteira do resultado, 0;

0,722 x 2 = 1,444 -> registra a parte inteira, 1;

0,444 x 2 = 0,888 -> registra a parte inteira, 0;

0,888 x 2 = 1,776 -> registra a parte inteira, 1;

Portanto, de cima para baixo, o número fracionário em binário é 0,0101

Resumindo:

·        Para converter um número inteiro decimal para binário, basta dividi-lo sucessivamente por 2, até o resto ser menor do que a base, e juntar os restos da divisão, do último para o primeiro.

·        Para converter um número binário para decimal, basta multiplicar os dígitos binários pela potência de 2 correspondente à posição de cada dígito e somar os resultados, como no primeiro exemplo anterior.

·        Para converter um número decimal fracionário, basta multiplicar a parte fracionária por 2 e registrar cada 0 ou 1 da parte inteira resultante, repetindo o processo para quantos bits desejarmos armazenar, como no segundo exemplo anterior.

Observação: A soma de números binários é parecida com a de números decimais, só que usando apenas os algarismos 0 e 1.

0 + 0 = 0

0 + 1 = 1

1 + 0 = 1

1 + 1 = 0 (e vai um)

Veja este último resultado:

   (+1)

0   1

0   1 +

_____

1   0

3 – Representação de dados em binário

Os computadores trabalham internamente com números binários. Todo dado que é manipulado por um programa de computador precisa ser representado internamente por um número binário, na memória dele.

Os programas podem usar dados dos tipos inteiros, decimais (floats), lógicos, strings, caracteres etc. Portanto, todos estes tipos de dados precisam ser representados em binário para armazenamento.

Cada computador define o tamanho da palavra de dados que irá trabalhar, que depende do microprocessador a ser utilizado. Os primeiros microprocessadores eram de 4 bits, mas depois passaram para 8 bits, 16 bits etc.

No segundo exemplo acima, o número decimal 107 foi representado pelo binário 01101011, que tem 8 bits (ou 1 byte). Caso o computador tivesse uma palavra de 16 bits, o mesmo número seria representado por 16 dígitos binários, assim:

00000000 01101011.

Agora vamos ver como cada tipo de dados deste é representado em binário.

Inteiros positivos (ou números naturais)

Um inteiro positivo é representado exatamente como no exemplo acima. Os zeros e uns preenchem todos os espaços reservados no conjunto, de acordo com os valores das potências de 2 do número binário, após a conversão do decimal equivalente.

Deste modo, para uma palavra de 8 bits, podem ser representados 256 números decimais positivos diferentes, entre 0 (00000000) e 255 (11111111).

0 0 0 0 0 0 0 0: decimal 0

0 0 0 0 0 0 0 1: 1

...

1 1 1 1 1 1 1 0: 254

1 1 1 1 1 1 1 1: 255

Inteiros negativos

Existe mais de uma maneira de se representar números inteiro negativos em binário, mas eu vou tratar aqui apenas daquela mais utilizada pela maioria dos computadores, o Complemento de 2.

Esta técnica consiste em inverter todos os bits (de 0 para 1 e vice-versa) do número inteiro positivo equivalente e, depois, somar 1 a ele.

Por exemplo, para representar o número -12 em uma palavra de 8 bits, faríamos o seguinte:

0 0 0 0 1 1 0 0 – número inteiro positivo, decimal 12

1 1 1 1 0 0 1 1 –> número com os bits invertidos

0 0 0 0 0 0 0 1 –> número decimal 1, para somar com o anterior

1 1 1 1 0 1 0 0 –> soma dos 2 números acima, representando o decimal -12

Se o primeiro bit (mais à esquerda) for 0, o número é um inteiro positivo, caso seja 1, será negativo. Desta forma, os 256 números inteiros que podem ser representados em uma palavra de 8 bits são:

0 0 0 0 0 0 0 0: 0

0 0 0 0 0 0 0 1: 1

0 0 0 0 0 0 1 0: 2

...

0 1 1 1 1 1 1 0: 126

0 1 1 1 1 1 1 1: 127

1 0 0 0 0 0 0 0: -128

1 0 0 0 0 0 0 1: -127

...

1 1 1 1 1 1 1 0: -2

1 1 1 1 1 1 1 1: -1

Veja que temos o zero (0), 127 números positivos e 128 números negativos.

Observação: se eu tenho um número decimal inteiro positivo e quero saber como representar o negativo equivalente, uso a técnica de complemento de 2.

E se eu tiver um número decimal inteiro negativo (1º bit é 1) e quero saber qual o número decimal positivo ele representa, também uso a mesma técnica.

Por exemplo, para saber qual número decimal negativo o número binário 10010101 representa, em uma palavra de 8 bits, faríamos o seguinte:

1 0 0 1 0 1 0 1 –> número binário inteiro negativo

0 1 1 0 1 0 1 0 –> número com os bits invertidos

0 0 0 0 0 0 0 1 –> número decimal 1, para somar com o anterior

0 1 1 0 1 0 1 1 –> soma dos 2 números acima, representando o decimal positivo 107

Ou seja, o binário negativo 10010101 representa -107 em decimal.

Caracteres

Desde os primeiros computadores, os caracteres são representados por códigos (EBCDIC, ASCII), que associam cada um deles a um valor numérico (decimal), também representado em binário (ou hexadecimal).

Hoje existem mais códigos e um dos mais usados é o Unicode e, para representar caracteres da língua portuguesa, o UTF-8, mas estes outros códigos ficam para um próximo artigo.

O código ASCII (“American Stardard Code for Information Interchange”) - ou código padrão americano para intercâmbio de informações, em tradução livre -, sempre foi o mais usado e ainda é usado nos computadores modernos.

Ele é baseado no alfabeto romano e sua função é padronizar a forma como os computadores representam letras, números, acentos, sinais diversos e alguns códigos de controle.

Neste código, os caracteres são divididos em categorias e são tabulados como números positivos representados em 8 bits. Portanto, é possível representar até 256 códigos diferentes (2⁸ possibilidades).

Cada caractere da tabela tem um código numérico decimal, mas também é representado pelo código equivalente em hexadecimal.

Resumindo a tabela, os primeiros 13 caracteres são dedicados a controle de impressora (exemplo, CR, LF, e outros) e existem códigos para vários caracteres de sinais de pontuação e acentuação, armazenados em sequências diferentes.

No entanto, os caracteres mais significativos (e os mais usados em programação) são estes:

·        Algarismos decimais (0 -> 9) – códigos 48 a 57 (em hexa, de x30 a x39);

·        Letras maiúsculas (A -> Z) - códigos 65 a 90 (em hexa, de x41 a x5A);

·        Letras minúsculas (a -> z) - códigos 97 a 122 (em hexa, de x61 a x7A);

A tabela ASCII básica, com os primeiros 128 caracteres é mostrada abaixo, com os caracteres, os números decimais:

Existe uma tabela com o código ASCII estendido, completando os 256 códigos possíveis, como mostra esta outra figura, mas seu detalhamento também vai ficar para outro artigo.

Números decimais fracionário (do tipo float ou double)

Uma das principais representações para números fracionários, ou seja, com uma parte inteira e outra fracionária (representado em linguagens de programação pelos tipos float e double) é o padrão IEEE 754.

Ela separa um número em mantissa e expoente, de maneira semelhante à notação científica. A mantissa representa a parte inteira e fracionária, enquanto o expoente eleva a base (2) ao expoente.

Por exemplo, o número decimal 123,456 pode ser representado pela notação científica: 1,23456 x 10² (o 1 andou 2 casas para a direita, 10²).

Da mesma forma, o número binário 110,001 pode ser representado pela notação científica: 1,10001 x 2² (o 1 andou 2 casas para a direita, 2²)

O padrão IEEE 754 para números de precisão simples (float) reserva 32 bits, 1 para o sinal, 8 para a mantissa e 23 para o expoente (ver figura abaixo). No caso de precisão dupla (double), são reservados 64 bits, 1 para o sinal, 11 para a mantissa e 52 para o expoente.

 O sinal será 0 para números positivos e 1 para negativos.

A mantissa deve conter as partes inteira e fracionária do número a ser representado, da mesma forma vista nos exemplos do início do artigo, lembrando que bits 0 à esquerda da parte inteira não são significativos, bem como à direita da parte fracionária.

IMPORTANTE: a parte inteira da mantissa sempre será o binário 1, devendo o número original ser deslocado para se chegar neste valor. Além disso, este valor 1 inicial ficará implícito, não sendo representado, mas só a parte fracionária.

O expoente do número a ser representado (já considerando que a parte inteira está com o binário 1) deve ser adicionado a 127 e só depois, será armazenado.

Desta forma, se o expoente do número for 0, será armazenado o valor 127 (0 + 127), se for -127, será armazenado o valor 0 (-127 + 127), se for 100, será armazenado o valor 227, e assim por diante.

Exemplo 1: como representar o número decimal 6,25 na forma do IEEE 754?

sinal do número -> 0 (número positivo);

mantissa, parte inteira -> decimal 6 = 0b110 (4 + 2);

mantissa, parte fracionária -> decimal 0,25, logo:

0,25 x 2 = 0,5 -> 0

0,5 x 2 = 1,0 -> 1

0 x 2 = 0...

Então, mantissa = 110,01

Deslocando para a direita, até o inteiro ficar só a unidade (1) -> 1,101 x 2²

Então, a mantissa que será representada será só a parte fracionária: 0,101

Este valor será preenchido por zeros á direita para completar o campo de 23 posições.

Expoente -> 2 + 127 = 129, em binário positivo fica 0b10000001

Logo, será armazenado 01000000110100000000000000000000 (sinal, expoente, mantissa)

Exemplo 2: qual é o número de ponto flutuante representado pelo binário

0b01000000011000000000000000000000, armazenado com a técnica IEEE 754?

Separando este número (0b1000000011000000000000000000000) nos diversos campos:

sinal do número -> 0 (1º bit, número positivo);

expoente -> 100 0000 0 (8 bits seguintes, decimal 128), fazendo 128 - 127 = 1;

mantissa -> 11000000000000000000000

mantissa, parte fracionária -> 0.11000000000000000000000 = 0,11

Mas 0,11 = 1 x 2^-1 + 1 x 2^-2 = 0,5 + 0,25 = 0,75

mantissa, parte inteira -> inteiro 1, implícito

Logo, mantissa -> 1,75

Então, a mantissa vale 1,75, o expoente 1 e o sinal 0 (positivo), de modo que o número representado é 1,75 x 2¹ = 1,75 x 2 = 3,5

4 – Considerações finais

Este é mais um artigo da série DIRETO AO PONTO, que eu estou escrevendo para a DIO. Ele tratou da representação de dados usados por um programa de computador para a forma binária, como eles são armazenados internamente em um computador.

Primeiramente, foram apresentadas as formas de se representar um inteiro positivo (números naturais), depois os inteiros negativos, caracteres e, por fim, os números fracionários.

Desta forma, pudemos ver como são representados internamente os dados das variáveis dos tipos inteiro, caracteres (e strings) e float (ou double).

Nos próximos artigos, veremos como operar com estes números binários, dando mais uma visão de como as coisas acontecem por baixo dos panos nos nossos computadores, quando programamos.

É o que chamamos de “escovar bits”!

Até o próximo artigo.

5 – Referências

[1] CARTER Nicholas, Schaum’s Outline of Computer Architecture. McGraw-Hill, 2002.

Artigos desta série: ( < ) Anterior | Índice | Seguinte ( > )