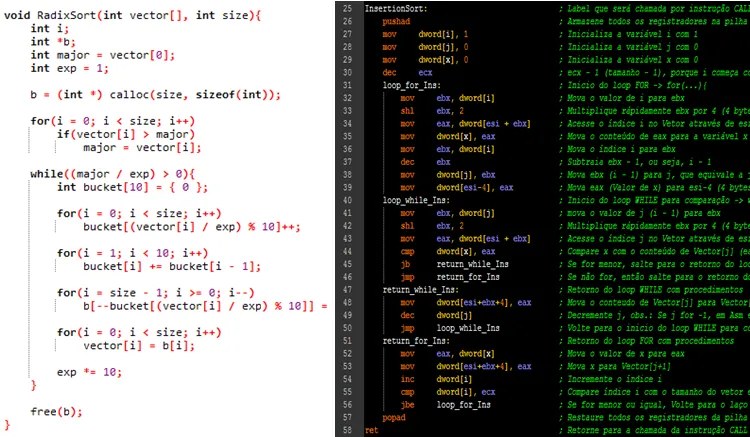
Algoritmos de Ordenação em C & Assembly
- #Estrutura de dados
- #C++
- #C
Olá pessoal! Venho trazer um artigo aqui que é muito essencial pra quem estuda a área de programação e que pode nos ajudar em diversas maneiras, falo sobre os Algoritmos de Ordenação ou também chamados de Métodos de Ordenação. No final deste artigo deixarei os links dos códigos pra vocês explorarem e também indico fortemente para aqueles que estão estudando lógica de programação ou iniciando nesta área que consultem os códigos, já percebi que esta é uma das boas formas de afiar nossa mente na lógica computacional! Como uma das frases que guardo comigo: “De nada importa a ferramenta/linguagem se não há compreensão da lógica por trás de todo o processo - Autor Desconhecido.” Mas chega de enrolação e vamos lá!
Digamos que você precise buscar em uma lista de dados, um registro telefônico cuja identificação é um nome, é uma lista gigantesca e os nomes não estão ordenados em ordem alfabética. Outro exemplo é você ter um sistema que classifica um grande número de indivíduos por faixa etária, porém esta lista está organizada por ordem alfabética dos nomes e você precisa buscar certos nomes na lista com uma idade X. Nos 2 exemplos, você teria uma dificuldade enorme para encontrar o dado esperado e no caso dos 2 sistemas, ele poderia levar o tempo muito maior pra encontrar os dados, para isto é preciso organizar os dados (Nome ou Idade) em uma ordem no qual seja mais rápido pra ser encontrado.
A ordenação tem o objetivo de facilitar as pesquisas de um determinado elemento, assim como diz a estratégia algorítmica: “Primeiro coloque os números em ordem. Depois decidimos o que fazer.”. Existem inúmeras técnicas algoritmicas para ordenar um Vetor, cada técnica com suas particularidades, Então vamos conhecer as classificações e tipos dos algoritmos de ordenação:
Troca: Os algoritmos de troca consiste em realizar comparações entre 2 valores em um Vetor e efetuar a troca dos valores nas posições, Exemplo: Se temos o número 9 na posição 3 do Vetor e o número 2 na posição 7 do Vetor, cuja condição é realizar a troca se o 1ª for maior que o 2ª, então após a troca, a posição 3 ficará com 2 e a posição 7 ficará com 9. Neste quesito, o algoritmo pode ler e comparar os próximos valores para possíveis trocas. Exemplos de Algoritmos de Troca: Bubble sort, Cocktail sort, Odd-even sort, Comb sort, Gnome sort e Quicksort
Seleção: Já a seleção, ao invés de apenas realizar trocas sucessivas mediante uma comparação, permite selecionar um determinado valor no Vetor que poderá servir como "Base" para os demais. Então digamos que precisamos procurar o 1ª maior valor do vetor, após encontrarmos, selecionamos a posição deste Vetor e colocamos ele no topo do Vetor, fazemos as comparações pra encontrar o 2ª maior valor do Vetor e encontrando, selecionamos o índice deste novo valor e assim por diante. Este pode ser um dos exemplos de Seleção e os conhecidos deste tipo são: Selection sort, Heapsort e Smoothsort.
Inserção: Os Algoritmos de Inserção envolve a seguinte regra: A cada novo valor, inseri-lo na posição correta diretamente. Para o algoritmo descobrir qual é a posição correta, ele precisa a cada valor comparar com todos os possíveis valores do vetor, ele será inserido depois ou antes de cada item a depender se for menor ou maior. Exemplo: Se em um Vetor de 12 posições, o número 9 foi lido no ínicio do vetor, ele compara com o item da posição seguinte, o item é menor, logo o algoritmo empurra este item menor pra esquerda, comparando e empurrando os próximos itens até encontrar um maior, sendo maior, o 9 será inserido naquela posição e isto seria feito para todos os números lidos em posições incorretas. Os Algoritmos que utilizam esta metodologia são: Insertion sort e Shell sort.
Mesclagem: A idéia dos Algoritmos de Mesclagem é dividir um problema em partes menores e resolve-los através de recursividade. Depois de resolvidos, o algoritmo "Mescla" todos os subproblemas resolvidos, neste caso, os vetores ordenados, construindo assim um só vetor. Esta resolução do problema final é chamada de "Conquista", por isto chamamos esta estratégia de "Divisão e Conquista", ou seja, Dividir os vetores em 2 ou mais partes, ordenar cada parte e depois mesclar todas as partes (Conquistar). Um algoritmo recorrente que utiliza esta estratégia é o QuickSort, porém o QuickSort não divide o problema em Sub-vetores diferentes e sim, divide o problema através do Pivô de base no mesmo vetor, justamente por isto o QuickSort não pode ser considerado um "Algoritmo de Mesclagem", os considerados são: Merge sort, Strand sort e Timsort
Humorísticos: Como o próprio nome já diz, a ideia é ser um algoritmo levado ao "Humor". São algoritmos extremamente ineficientes e que não são utilizados na prática e sim da forma didática para ensinar sobre o que é "Eficiência". Um Exemplo é o BogoSort que baseia a sua ordenação em uma Reordenação aleatória dos elementos. Um algoritmo probabilístico por natureza e se todos os elementos a serem ordenados são distintos entre si, a complexidade esperada é O(n x n!), isto é, com n elementos, seria "n vezes fatorial de n" comparações. E não precisamos nem falar que existe uma certa "probabilidade" do algoritmo NUNCA conseguir ordenar os valores. Por isto outro nome dado ao BogoSort é "Estou com Sorte". Outro algoritmo nesta mesma classificação de humor é o StoogeSort, que utiliza a técnica de divisão e conquista, com uma diferença: Ordenar inúmeras vezes um vetor que já estaria ordenado, o que o faz ser consequentemente mais lento que os algoritmos mais simples, por isso não é indicado sua utilização.
Após vermos os tipos e classificações de algoritmos, veremos sobre 2 métodos de algoritmos: O Método Simples e o Método Eficiente.
Métodos Simples
Os métodos mais simples são aqueles que são bem fáceis de entender e que são mais recomendados para matrizes pequenas. Exemplos: SelectionSort, InsertionSort, BubbleSort e CombSort. Possuem complexidade C(n) = O(n²), isto é, baseado em n elementos no vetor, n² comparações serão feitas para a ordenação completa. Apesar de serem "fáceis", não são adequados para ordenação de grande volume de dados. Veremos alguns deles:
InsertionSort - A missão do Insertion é percorrer todo o array, capturando valor por valor, cada valor será uma nova carta. Então imaginemos que estamos com um baralho desordenado nas mãos e pegamos a 2ª carta, vamos comparar esta carta com as anteriores e se for menor, posicionamos esta carta antes das maiores, e depois fazemos este mesmo processo para a 3ª carta, posicionando-a antes de uma carta maior, e assim pra 4ª carta, 5ª, etc... No final todo o nosso baralho está ordenado. Esta é a ideia da "Inserção" que é identificar o próximo valor e inserir na posição anterior de uma posição que estava com um número maior, a medida que o algoritmo executa, os números maiores vão se deslocando para a direita e os números menores se deslocando para a esquerda. No melhor caso possui complexidade C(n) = O(n) e no médio e pior caso C(n) = O(n²). É considerado um método de ordenação estável.

SelectionSort - É um algoritmo de ordenação por seleção, cuja responsabilidade é passar o menor valor do Array para a 1ª posição, após isto colocar o 2ª menor valor do Array na 2ª posição, 3ª menor valor na 3ª posição e assim é feito para os (n - 1) elementos restantes. Para o algoritmo saber qual é o menor valor em cada ordem (1ª, 2ª,... Nª), ele precisa de um laço externo que "seleciona" o valor do índice inicial e um laço interno que percorre todo o Array, quando é encontrado o 1ª menor valor, o algoritmo seleciona a posição atual onde o menor valor está e faz a troca de valores das posições selecionadas, a partir daí o próximo índice inicial é selecionado pelo laço externo e o mesmo processo novamente é feito com o laço interno, até que sobre os 2 últimos valores restantes, que se forem menor, a troca será feita, se não, continuarão como estão. Para todos os casos (Melhor, Médio e Pior) possui complexidade C(n) = O(n²) e não é um algoritmo estável.

Métodos Eficientes
Os métodos eficientes são bem mais complexos que os mais simples, porém com a vantagem de exigir um número menor de comparações, o que os torna mais rápidos. Projetados para trabalhar com uma grande quantidade de dados, os métodos eficientes possuem complexidade C(n) = O(n log n), que se lê "Logarítmo de n na base n" comparações, Exemplo: Se temos um vetor de 8 elementos, logo n = 8, então log de 8 na base 8 é igual a 1, que seria 1 comparação no melhor caso, sendo o pior caso O(n²). Exemplo de algoritmos: Quick sort, Merge sort, Shell sort, Heap sort, Radix sort, Gnome sort, Cocktail sort e Timsort. Abaixo 2 destes algoritmos do método eficiente:
QuickSort - O QuickSort é um algoritmo rápido e eficiente baseando na estratégia de "Divisão e Conquista" que consiste em dividir o vetor em 2 metades através de um elemento chamado "Pivô". Este elemento fica na metade do vetor principal (ou em sub-vetores), o QuickSort se encarrega de percorrer todo o vetor colocando os elementos menores que o pivo na metade esquerda e os elementos maiores que o pivo na metade direita, após isto, é feito uma ou mais chamadas recursivas da função para fazer o mesmo procedimento na metade esquerda, dividindo e ordenando várias vezes até que toda a metade esquerda do vetor principal esteja ordenada. Uma 2ª chamada recursiva é feita para ordenar todos as metades direitas com o mesmo processo, até que o algoritmo comece a passar pro lado direito do vetor principal. A ideia deste algoritmo é dividir um problema original em subproblemas que possam ser resolvidos de forma mais fácil e rápida. No pior caso possui complexidade C(n) = O(n²) e no médio e melhor caso C(n) = O(n log n), O quicksort é um algoritmo de ordenação por comparação não-estável.

RadixSort - Este é um dos meus preferidos baseando na sua estratégia. O Radix sort é um algoritmo de ordenação rápido e estável que pode ser usado para ordenar itens que estão identificados por chaves únicas. Cada chave é uma cadeia de caracteres ou número, e o radix sort ordena estas chaves em qualquer ordem relacionada com a lexicografia. Na ciência da computação, radix sort é um algoritmo de ordenação que ordena inteiros processando dígitos individuais. Como os inteiros que podem representar strings compostas de caracteres (como nomes ou datas) e pontos flutuantes especialmente formatados, radix sort não é limitado somente a inteiros. O algoritmo de ordenação radix sort foi originalmente usado para ordenar cartões perfurados. Um algoritmo computacional para o radix sort foi inventado em 1954 no MIT por Harold H. Seward.
De uma forma mais simples e didática: O Algoritmo Radix cria um vetor auxiliar de 10 posições e sabemos que cada posição tem um índice numérico. O Algoritmo percorre todo o vetor principal, capturando o 1ª dígito de cada elemento no vetor principal e a cada 1ª dígito será o índice do vetor auxiliar cujo conteúdo será incrementado +1 na iteração. Após percorrer todo o vetor principal, cada número resultante incrementado no vetor auxiliar (começando da 1ª posição) será somado + o número na 2ª posição, dando o resultado na 2ª posição e a 2ª posição somada com a 3ª dando o resultado para 3ª posição e assim por diante, até o último valor do vetor auxiliar. Após isto, o algoritmo volta a ler o vetor principal ao inverso, pegando o 1ª dígito de cada elemento, servindo como índice do vetor auxiliar e neste índice, o conteúdo será a índice do vetor principal onde o elemento atual será colocado, no final da leitura inversa, todo o vetor já foi organizado. Abaixo está a demonstração do RadixSort:
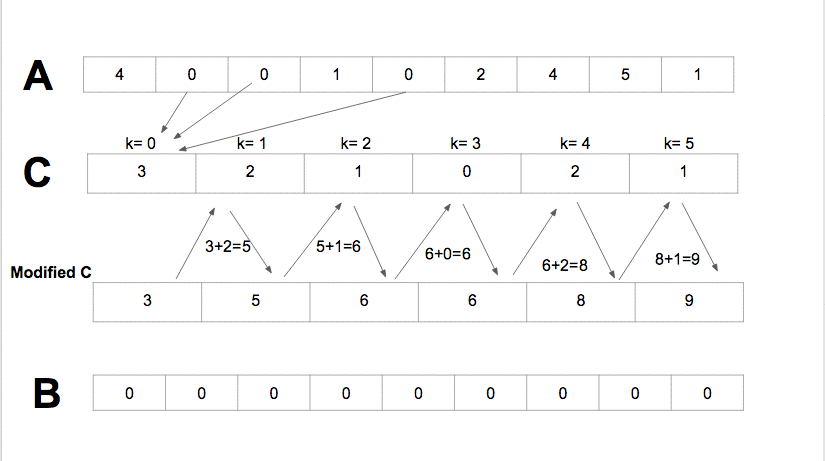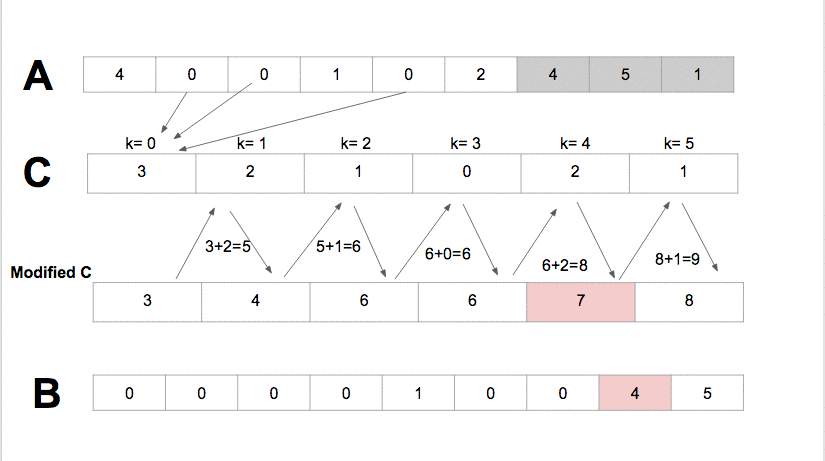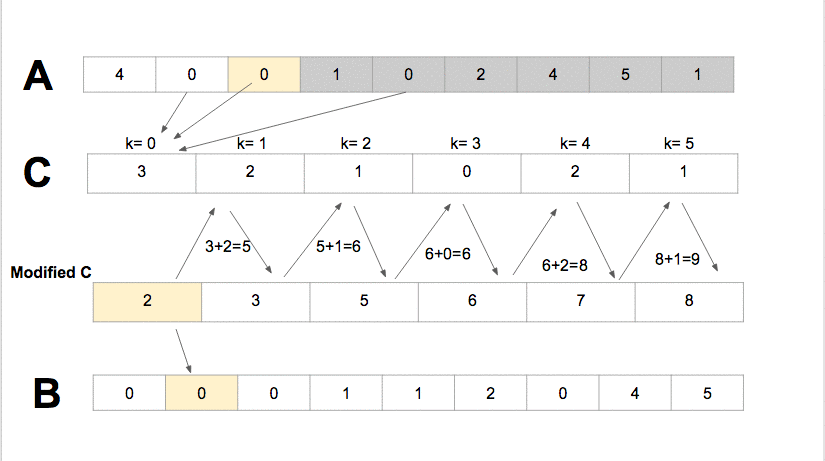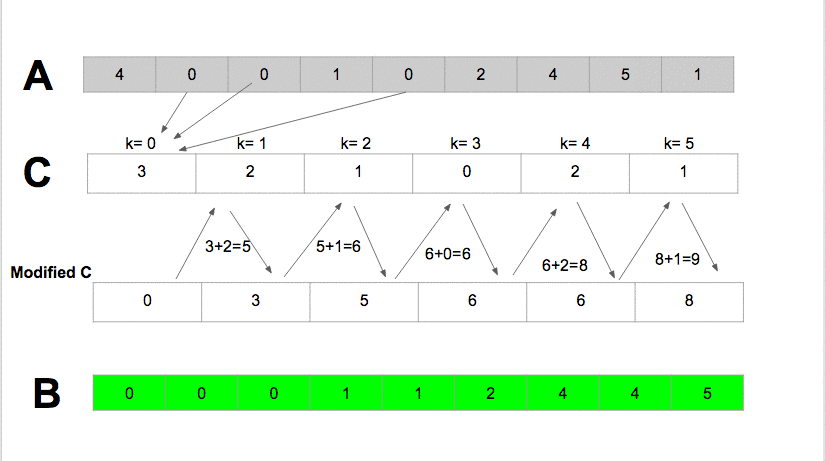
Eu fiz 2 repositórios com 17 algoritmos distintos de ordenação - 1 Repositório com os algoritmos na linguagem C e o outro na linguagem Assembly. No repositório da linguagem C há uma aplicação EXE com as chamadas de todos os algoritmos. No Entanto, na linguagem Assembly só trabalhei em 3 algoritmos: O InsertionSort, SelectionSort e o QuickSort, ainda estou trabalhando nos outros. Em Assembly, as rotinas dos algoritmos ocorrem em um sistema bootável, fora do sistema operacional, então pra executá-los será necessário algumas ferramentas como a "Máquina Virtual" por exemplo, abaixo vou deixar os links dos repos e do curso no Youtube que ensino como criar um sistema operativo/bootável em Assembly:
Algoritmos em C:
github.com/FrancisBFTC/C_Sorting_Algorithms
Algoritmos em Assembly:
github.com/FrancisBFTC/ASM_Sorting_Algorithms
Curso de Sistema Operacional em Assembly:
www.youtube.com/Desenvolvendo_Seu_Sistema_Operacional
Se puderem me dar um voto neste artigo eu agradeço de coração! <3 Sigam lá no github e deêm um Fork para se manterem atualizados de novos algoritmos que vou estar postando. Em breve farei um artigo de "Algoritmos de Criptografia", Valeu galera!!
#assembly #bios #linguagemC #programação